【基礎知識】乃木坂46の「いつかできるから今日できる」を数学的命題として解釈する
- 命題
基礎知識
基礎知識
ここでは数学1の「三角比」についてまとめています。
三角比は数学2で学習する三角関数の基礎でありつつ、単元を問わず広く利用されていますので、しっかり学習しておきましょう。
目次
公開までしばらくお待ちください。
公開までしばらくお待ちください。
三角比計算の一番の基本となる三角比の相互関係式の説明を行っています。
【公式】三角比の相互関係式について
三角比に関する公式はとても多く、しかも覚えにくいという特徴があります。
しかし、それは単純暗記に頼ってしまうことが原因です。
三角比に限ったことではありませんが、各種公式の導出方法自体を覚え、その場で公式の導出を行えるような実力をつけることを目指しましょう。
【公式】三角比の各種公式
ただし、 $R$ は三角形 $ABC$ の外接円半径
正弦定理を理解するには三角比よりも円周角の知識が重要となります。
しかし円周角についての知識は中学数学の内容で事足りますので、きっと理解できることでしょう。
【三角比】正弦定理の証明
三角比に関する重要な定理といえば「正弦定理」と「余弦定理」の二つになります。
三角形を計量するために必須となるこの二つの定理は、「道具」として重宝します。
道具としてすぐに使うためには、式の形を暗記している必要があるのですが、なぜそのような式が成り立つのかを知っていることも大切です。
【三角比】余弦定理の証明
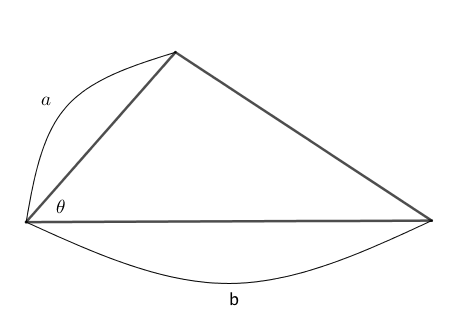
上図の三角形の面積 $S$ は、
$$\begin{array}{rcl} S = \cfrac{1}{2}~ab \sin \theta \\\\ \end{array}$$三角形の面積は「底辺 × 高さ ÷ 2」だけでなく、ここで紹介した方法で求める機会も多くなりますので、自在に扱えるように練習しておきましょう。
三角比を用いた三角形の面積の求め方
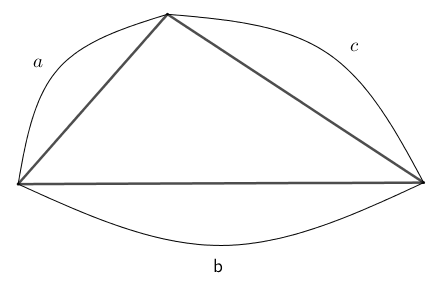
上図の三角形の面積 $S$ は、
$$\begin{array}{rcl} S &=& \sqrt{s(s-a)(s-b)(s-c)} \end{array}$$ただし、 $s = \cfrac{a+b+c}{2}$
ヘロンの公式は、三角形の3辺の長さから面積を求めるための公式です。
ヘロンの公式は、辺の長さだけで面積が求められるという点については有用なのですが、辺の長さに無理数が含まれる場合などは計算が煩雑になる場合があります。
またヘロンの公式は、三角比に関する基礎的かつ必須の重要公式をもとに成立しているという背景もありますので、ヘロンの公式に頼りすぎず、三角比の各種公式だけを用いて面積を求められるようにしておきましょう。
ヘロンの公式の証明
公開までしばらくお待ちください。
その他の基礎知識は後日追加予定です。
数学Iの目次
この記事が気に入ったら
「いいね」しよう!
-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。
>> お問い合わせ
>> プライバシーポリシー