【基礎知識】乃木坂46の「いつかできるから今日できる」を数学的命題として解釈する
- 命題
基礎知識
公式
数列の和とΣ記号
ここでは $\sum$ を用いた数列の和の表現方法と、 $\sum$ を用いた重要公式についての解説を行います。
複雑な計算が要求され、Σという記号自体もとっつきにくいものではありますが、基礎から理解していきましょう。
Σとは
$\sum$ は「シグマ」と読み、英語で意味するところの和（ $ =Sum$ ）の頭文字「 $S$ 」に対応するギリシャ文字です。
例えば、数列 $\{a_n\}$ の初項から第 $n$ 項までの和は $\sum$ を用いて次のように表すことができます。
$$\begin{array}{rcl} a_1 + a_2 + \cdots + a_n &=& \displaystyle \sum_{k=1}^n a_k \\\\ \end{array}$$$k, 1, n$ の意味は下のようになります。
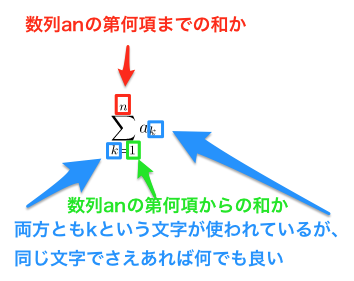
上図を踏まえると、
$$\begin{array}{rcl} \displaystyle\sum_{k=1}^n a_k &=& \displaystyle\sum_{l=1}^n a_l \\\\ \end{array}$$や、
$$\begin{array}{rcl} a_2 + a_3 + \cdots + a_7 &=& \displaystyle\sum_{k=2}^7 a_k \\\\ \end{array}$$が成り立つことがわかるかと思います。
Σの性質
和のΣはΣの和
Σの性質として次の式が成り立ちます。
$$\begin{array}{rcl}
\displaystyle\sum_{k=1}^n ~(a_k + b_k) &=& \displaystyle\sum_{k=1}^n a_k + \displaystyle\sum_{k=1}^n b_k \\\\
\end{array}$$
証明
$\displaystyle\sum_{k=1}^n ~(a_k + b_k) \\$
$= (a_1 + b_1) + (a_2 + b_2) + \cdots + (a_n + b_n) \\$
$= (a_1 + a_2 + \cdots + a_n) + (b_1 + b_2 + \cdots + b_n) \\$
$= \displaystyle\sum_{k=1}^n a_k + \displaystyle\sum_{k=1}^n b_k \\$
以上により、
$$\begin{array}{rcl}
\displaystyle\sum_{k=1}^n ~(a_k + b_k) &=& \displaystyle\sum_{k=1}^n a_k + \displaystyle\sum_{k=1}^n b_k
\end{array}$$
が証明されました。
積のΣはΣの積
Σの性質として次の式が成り立ちます。
$p$ は $k$ に無関係な定数のとき、
$$\begin{array}{rcl} \displaystyle\sum_{k=1}^n pa_k &=& p \displaystyle\sum_{k=1}^n a_k \\\\ \end{array}$$証明
マスマスターの思考回路
以上により、
$$\begin{array}{rcl}
\displaystyle\sum_{k=1}^n pa_k &=& p \displaystyle\sum_{k=1}^n a_k
\end{array}$$
が証明されました。
Σを用いた累乗の和の公式
$$\begin{array}{rcl}
&& 1. ~~ \displaystyle\sum_{k=1}^n k = \cfrac{n(n+1)}{2} \\\\
&& 2. ~~ \displaystyle\sum_{k=1}^n k^2 = \cfrac{n(n+1)(2n+1)}{6} \\\\
&& 3. ~~ \displaystyle\sum_{k=1}^n k^3 = \left \{ \cfrac{n(n+1)}{2} \right \}^2 \\\\
\end{array}$$
1の証明
$$\begin{array}{rcl} \displaystyle\sum_{k=1}^n k &=& 1 + 2 + \cdots + n \\\\ \end{array}$$マスマスターの思考回路
上式の右辺は、初項1, 交差1の等差数列の初項から第 $n$ 項までの和に一致します。
等差数列の和の公式より、
$$\begin{array}{rcl} S_n &=& \cfrac{ n\{2a + (n-1)d \} }{2} \\\\ \end{array}$$を用いると、
$$\begin{array}{rcl} 1 + 2 + \cdots + n &=& \cfrac{ n\{2 \cdot 1 + (n-1) \cdot 1 \} }{2} \\\\ &=& \cfrac{ n\{2 + (n-1) \} }{2} \\\\ &=& \cfrac{ n(n+1)}{2} \\\\ \end{array}$$以上により、
$$\begin{array}{rcl}
\displaystyle\sum_{k=1}^n k = \cfrac{n(n+1)}{2}
\end{array}$$
が証明されました。
2の証明
マスマスターの思考回路
三乗の展開公式を用いた証明方法が有名ですが、三乗の展開公式を用いるという証明方針が難解なため、この公式については公式そのものを丸暗記してしまう事がおすすめです。
三乗の展開公式より
$$\begin{array}{rcl} (k+1)^3 &=& k^3 + 3k^2 + 3k +1 \\\\ (k+1)^3 – k^3 &=& 3k^2 + 3k +1 \\\\ \end{array}$$上式に $k = 1, 2, \cdots, n$ を代入すると、
$$\begin{array}{rcl} 2^3 – 1^3 &=& 3 \cdot 1^2 + 3 \cdot 1 +1 \\\\ 3^3 – 2^3 &=& 3 \cdot 2^2 + 3 \cdot 2 +1 \\\\ 4^3 – 3^3 &=& 3 \cdot 3^2 + 3 \cdot 3 +1 \\\\ \cdots &=& \cdots \\\\ (n+1)^3 – n^3 &=& 3n^2 + 3n +1 \\\\ \end{array}$$上式の辺々を加えて整理すると、
$(n+1)^3 – 1^3 = 3(1^2 + 2^2 + 3^2 + \cdots + n^2) + 3(1 + 2 + 3 + \cdots + n) + 1 \cdot n \\$
$(n^3 + 3n^2 + 3n +1) – 1 = 3 \displaystyle\sum_{k=1}^n k^2 + 3 \displaystyle\sum_{k=1}^n k + n \\$
$n^3 + 3n^2 + 2n = 3 \displaystyle\sum_{k=1}^n k^2 + 3 \displaystyle\sum_{k=1}^n k \\$
ここで、
$\displaystyle\sum_{k=1}^n k = \cfrac{n(n+1)}{2} \\$
より、
$n^3 + 3n^2 + 2n = 3 \displaystyle\sum_{k=1}^n k^2 + \cfrac{3n(n+1)}{2} \\$
$3 \displaystyle\sum_{k=1}^n k^2 = n^3 + 3n^2 + 2n – \cfrac{3n(n+1)}{2} \\$
$= n(n^2 + 3n + 2) – \cfrac{3n(n+1)}{2} \\$
$= n(n+1)(n+2) – \cfrac{3n(n+1)}{2} \\$
$= \cfrac{2n(n+1)(n+2)}{2} – \cfrac{3n(n+1)}{2} \\$
$= \cfrac{n(n+1)}{2} \{ 2(n+2) – 3 \} \\$
$= \cfrac{n(n+1)}{2} (2n+4 – 3) \\$
$= \cfrac{n(n+1)}{2} (2n+1) \\$
両辺を3で割ると、
$\displaystyle\sum_{k=1}^n k^2 = \cfrac{n(n+1)(2n+1)}{6} \\$
以上により、
$$\begin{array}{rcl}
\displaystyle\sum_{k=1}^n k^2 = \cfrac{n(n+1)(2n+1)}{6}
\end{array}$$
が証明されました。
3の証明
マスマスターの思考回路
2の証明と同様に証明方針が難解なため、この公式についても公式そのものを丸暗記してしまう事がおすすめです。
二項定理を用いて4乗の展開を行います。
$$\begin{array}{rcl} (k+1)^4 &=& k^4 + 4k^3 + 6k^2 + 4k + 1 \\\\ (k+1)^4 – k^4 &=& 4k^3 + 6k^2 + 4k + 1 \\\\ \end{array}$$上式に $k = 1, 2, \cdots, n$ を代入すると、
$$\begin{array}{rcl} 2^4 – 1^4 &=& 4 \cdot 1^3 + 6 \cdot 1^2 + 4 \cdot 1 + 1 \\\\ 3^4 – 2^4 &=& 4 \cdot 2^3 + 6 \cdot 2^2 + 4 \cdot 2 + 1 \\\\ 4^4 – 3^4 &=& 4 \cdot 3^3 + 6 \cdot 3^2 + 4 \cdot 3 + 1 \\\\ \cdots &=& \cdots \\\\ (n+1)^4 – n^4 &=& 4n^3 + 6n^2 + 4n + 1 \\\\ \end{array}$$上式の辺々を加えて整理すると、
$(n+1)^4 – 1^4 = 4(1^3 + 2^3 + 3^3 + \cdots + n^3) + 6(1^2 + 2^2 + 3^2 + \cdots + n^2) + 4(1 + 2 + 3 + \cdots + n) + 1 \cdot n \\$
左辺を展開、右辺を$ \displaystyle\sum$ で表すと
$(n^4 + 4n^3 + 6n^2 + 4n +1) – 1 = 4 \displaystyle\sum_{k=1}^n k^3 + 6 \displaystyle\sum_{k=1}^n k^2 + 4 \displaystyle\sum_{k=1}^n k + n \\$
左辺を整理すると
$n^4 + 4n^3 + 6n^2 + 3n = 4 \displaystyle\sum_{k=1}^n k^3 + 6 \displaystyle\sum_{k=1}^n k^2 + 4 \displaystyle\sum_{k=1}^n k \\$
ここで、
$$\begin{array}{rcl} \displaystyle\sum_{k=1}^n k &=& \cfrac{n(n+1)}{2} \\\\ \displaystyle\sum_{k=1}^n k^2 &=& \cfrac{n(n+1)(2n+1)}{6} \\\\ \end{array}$$より、
$n^4 + 4n^3 + 6n^2 + 3n = 4 \displaystyle\sum_{k=1}^n k^3 + 6 \cfrac{n(n+1)(2n+1)}{6} + 4 \cfrac{n(n+1)}{2} \\$
$n(n^3 + 4n^2 + 6n + 3) = 4 \displaystyle\sum_{k=1}^n k^3 + n(n+1)(2n+1) + 2n(n+1) \\$
$4 \displaystyle\sum_{k=1}^n k^3 = n(n^3 + 4n^2 + 6n + 3) – n(n+1)(2n+1) – 2n(n+1) \\$
$= n\{(n^3 + 4n^2 + 6n + 3) – (n+1)(2n+1) – 2(n+1) \} \\$
$= n(n^3 + 4n^2 + 6n + 3 – 2n^2 – 3n -1 – 2n -2) \\$
$= n(n^3 + 2n^2 + n) \\$
$= n^2(n^2 + 2n + 1) \\$
$= n^2(n + 1)^2 \\$
両辺を4で割ると
$\displaystyle\sum_{k=1}^n k^3 = \cfrac{n^2(n + 1)^2}{4} \\$
$= \cfrac{n^2(n + 1)^2}{2^2} \\$
$= \left \{ \cfrac{n(n + 1)}{2} \right \}^2 \\$
以上により、
$$\begin{array}{rcl}
\displaystyle\sum_{k=1}^n k^3 = \left \{ \cfrac{n(n+1)}{2} \right \}^2
\end{array}$$
が証明されました。
定数のΣ
$c$ は $k$ に無関係な定数のとき、
$$\begin{array}{rcl} \displaystyle\sum_{k=1}^n c = nc \\\\ \end{array}$$証明
マスマスターの思考回路
$c$ は $k=1, 2, 3, \cdots, n$ のとき、常に $c$ なので
$c$ を $n$ 回足すことになります。
以上により、
$c$ は $k$ に無関係な定数のとき、
$$\begin{array}{rcl} \displaystyle\sum_{k=1}^n c = nc \end{array}$$が証明されました。
等比数列のΣ
$r \neq 1$ のとき、
$$\begin{array}{rcl} \displaystyle\sum_{k=1}^n r^{k-1} = \cfrac{1-r^n}{1-r} \\\\ \end{array}$$証明
$$\begin{array}{rcl} \displaystyle\sum_{k=1}^n r^{k-1} &=& r^0 + r^1 + \cdots + r^{n-1} \\\\ &=& 1 + r^1 + \cdots + r^{n-1} \\\\ \end{array}$$マスマスターの思考回路
上式の右辺は、初項1, 交比rの等比数列の初項から第 n 項までの和に一致します
等比数列の和の公式より、
$$\begin{array}{rcl} S_n &=& \cfrac{a(1-r^n)}{1-r} \end{array}$$を用いると、
$$\begin{array}{rcl} \displaystyle\sum_{k=1}^n r^{k-1} = \cfrac{1-r^n}{1-r} \\\\ \end{array}$$以上により、
$r \neq 1$ のとき、
$$\begin{array}{rcl} \displaystyle\sum_{k=1}^n r^{k-1} = \cfrac{1-r^n}{1-r} \end{array}$$が証明されました。
マスマスターの思考回路
等比数列について $r=1$ のときは、交差0の等差数列となりますので、定数のΣとして和を求めることができます。
数列の和とΣ記号の説明のおわりに
いかがでしたか？
$\displaystyle\sum_{k=1}^n k^2$ と $\displaystyle\sum_{k=1}^n k^3$ の公式は導出のアプローチが難しいので、公式を丸暗記することをおすすめします。
Σ計算は計算の難易度が高く、その見た目からしてとっつきにくいものではありますが、その知識が必要とされる場面は多くあります。
数式の意味を理解し、正しく計算できるように練習を積んでおきましょう。
【数列】数列のまとめ
この記事が気に入ったら
「いいね」しよう！
プロフィール
-このサイトの記事を書いている人-
某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。
お問い合わせ
>> お問い合わせ
>> プライバシーポリシー
$p$ は $k$ に無関係な定数なので、 $k$ の値によらず、常に $p$ という値をとります。