学校や塾では教えてくれない、元塾講師の思考回路の公開

公式

方べきの定理は覚えないようにしましょう

方べきの定理は、円と２直線が作る図形の線分の長さに関する定理です。

方べきの定理の式は複雑で覚えにくいのですが、基礎的な図形の知識を用いて導出することが可能なので、覚える必要はありません。

導出には補助線を引くという図形に対する「勘」が必要となりますが、それは方べきの定理の導出に限ったことではありませんので、ぜひ覚えずに対応できるようになることを目指しましょう。

方べきの定理

方べきの定理は次の3つのことを言います。

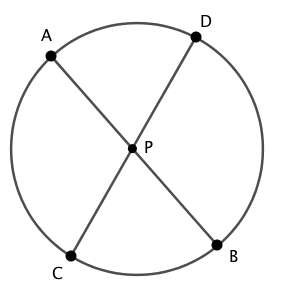
方べきの定理1

方べきの定理1

上図において、

    \begin{eqnarray*} PA \cdot PB &=& PC \cdot PD \end{eqnarray*}

が成り立つ

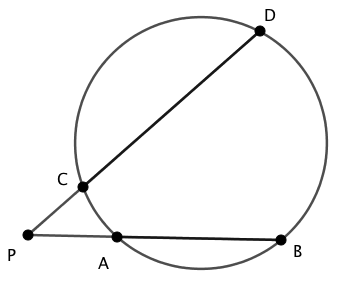
方べきの定理2

方べきの定理2

上図において、

    \begin{eqnarray*} PA \cdot PB &=& PC \cdot PD \end{eqnarray*}

が成り立つ

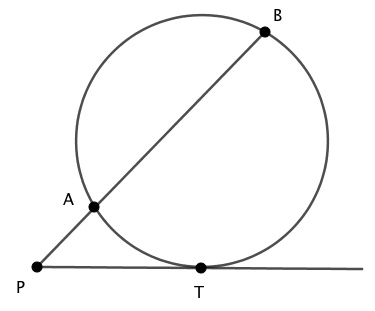
方べきの定理3

方べきの定理3

上図において直線 PT が円の接線であるとき、

    \begin{eqnarray*} PA \cdot PB &=& PT^2 \end{eqnarray*}

が成り立つ

方べきの定理の証明

方べきの定理1の証明

点 A と点 C および、 点 D と点 B を結びます。

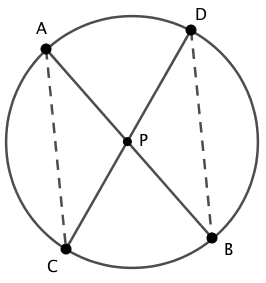
方べきの定理1の証明

\triangle{APC} と \triangle{DPB} において、

円周角の定理より、

\angle PAC = \angle PDB

\angle PCA = \angle PBD

2組の角がそれぞれ等しいので、

\triangle{APC} ∽ \triangle{DPB} が成り立つ。

相似な図形の対応する辺の比は等しいので、

    \begin{eqnarray*} PA : PD = PC : PB \end{eqnarray*}

よって、

    \begin{eqnarray*} PA \cdot PB &=& PC \cdot PD \end{eqnarray*}

が成り立つことが証明されました。

方べきの定理2の証明

点 A と点 D および、 点 C と点 B を結びます。

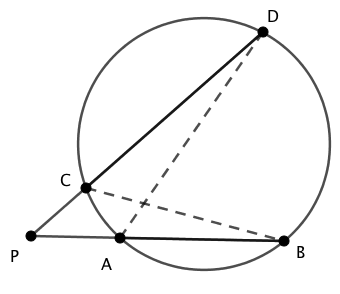
方べきの定理2の証明

\triangle{PAD} と \triangle{PCB} において、

円周角の定理より、

\angle ADP = \angle CBP

\angle P は共通。

2組の角がそれぞれ等しいので、

\triangle{PAD} ∽ \triangle{PCB} が成り立つ。

相似な図形の対応する辺の比は等しいので、

    \begin{eqnarray*} PA : PC = PD : PB \end{eqnarray*}

よって、

    \begin{eqnarray*} PA \cdot PB &=& PC \cdot PD \end{eqnarray*}

が成り立つことが証明されました。

方べきの定理3の証明

点 A と点 T および、 点 B と点 T を結びます。

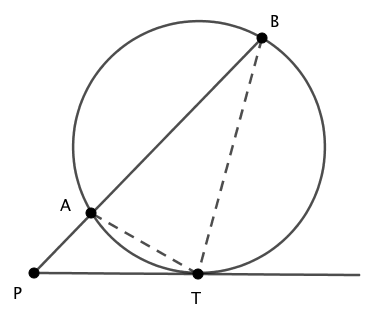
方べきの定理3の証明

\triangle{PAT} と \triangle{PTB} において、

接弦定理より、

\angle PTA = \angle PBT

【基礎】接弦定理の証明

\angle P は共通。

2組の角がそれぞれ等しいので、

\triangle{PAT} ∽ \triangle{PTB} が成り立つ。

相似な図形の対応する辺の比は等しいので、

    \begin{eqnarray*} PA : PT = PT : PB \end{eqnarray*}

よって、

    \begin{eqnarray*} PA \cdot PB &=& PT^2 \end{eqnarray*}

が成り立つことが証明されました。

方べきの定理の説明のおわりに

いかがでしたか？

接弦定理を用いることを除けば、方べきの定理は中学数学の範囲内で導出可能なものとお分りいただけたかと思います。

公式はなるべく覚えないで済ませることが、未知の問題に対応する力をつけるために役立ちますので、方べきの定理はぜひ覚えないでおきましょう。

公式との付き合い方について、詳しくは以下の記事を参考にしてください。

数学の公式は丸暗記しちゃダメ！公式は覚えるものではなく「証明」して作るものです

【基礎】図形の性質のまとめ

公式

図形の性質

プロフィール

-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。

検索

この記事の目次

関連記事

サイドメニュー