公式

チェバの定理は三角形の線分比に関する定理です。

本記事で紹介する初等幾何を用いた証明は着想が難解ですが、知識としては中学校で学習した内容で事足りますので、ぜひ読み進めてみてください。

チェバの定理

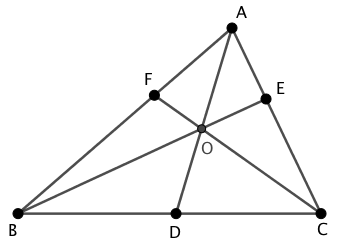
上図の三角形 $ABC$ について

がなりたつ。

チェバの定理の証明

三角形 $OAC$ と三角形 $OBC$ の面積比を考えます。

図を再掲します。

$OAC : OBC = (FAC – FAO) : (FBC – FBO) \\$
$= (FAC – \cfrac{FO}{FO + OC}~FAC) : (FBC – \cfrac{FO}{FO + OC}~FBC) \\$
$= \cfrac{OC}{FO + OC}~FAC : \cfrac{OC}{FO + OC}~FBC \\$
$= FAC : FBC \\$
$= AF : FB $

よって、

$$\begin{align} \cfrac{OBC}{OAC} &=& \cfrac{FB}{AF} \\ \end{align}$$

となります。

つまり下図のように、「青色と赤色の三角形の面積比は、青色と赤色の線分比に等しい」ということになります。

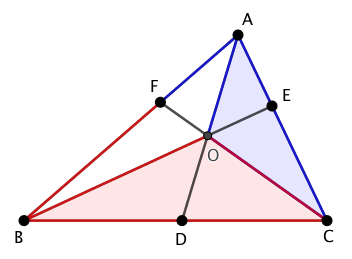
これを用いると、

$$\begin{align} \cfrac{OAC}{OAB} &=& \cfrac{DC}{BD} \\ \end{align}$$ $$\begin{align} \cfrac{OAB}{OBC} &=& \cfrac{EA}{CE} \\ \end{align}$$

が成り立ちます。

(1), (2), (3)式の各辺をそれぞれかけ合わせると

$$\begin{array}{rcl} \cfrac{OBC}{OAC} \cdot \cfrac{OAC}{OAB} \cdot \cfrac{OAB}{OBC} &=& \cfrac{FB}{AF} \cdot \cfrac{DC}{BD} \cdot \cfrac{EA}{CE}\\\\ 1 &=& \cfrac{FB}{AF} \cdot \cfrac{DC}{BD} \cdot \cfrac{EA}{CE}\\ \end{array}$$

以上により、

が証明されました。

チェバの定理の覚え方

三角形の頂点の名前は問題によって異なりますので、チェバの定理をそのまま記号として丸暗記してもうまく使えないことがあります。

下の図のように、適当に頂点を選び（この場合はA）、ぐるっと1周回るというように覚えておきましょう。

チェバの定理の説明のおわりに

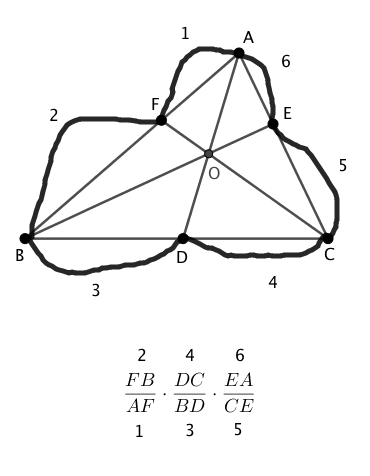
いかがでしたか？

チェバの定理の証明は着想が難しいですが、その定理自体を使いこなすことができれば良いかと思います。

また、チェバの定理とよく似たメネラウスの定理というものもありますので、これについても併せて勉強しておくとよいでしょう。

【図形】メネラウスの定理の証明と覚え方

【基礎】図形の性質のまとめ