学校や塾では教えてくれない、元塾講師の思考回路の公開

公式

【図形】メネラウスの定理の証明と覚え方

ここではチェバの定理によく似た、メネラウスの定理についての説明を行います。

似ているどころか式の形自体も同じになる場合もありますが、それぞれの定理が対象としている図形は異なるということに注意が必要でしょうか。

チェバの定理についてはをこちらをご覧ください。

【図形】チェバの定理の証明と覚え方

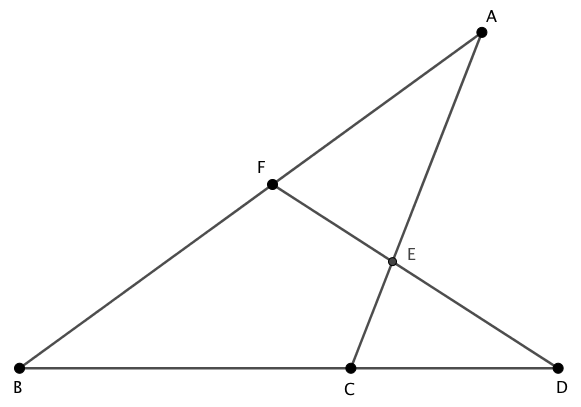
メネラウスの定理

メネラウスの定理

上図の三角形 ABC と線分 DF について

    \begin{eqnarray*} \cfrac{FB}{AF} \cdot \cfrac{DC}{BD} \cdot \cfrac{EA}{CE} &=& 1 \\\\ \end{eqnarray*}

がなりたつ。

メネラウスの定理の証明

下のように点 C, A, B から 直線 DF へ垂線を引きます。

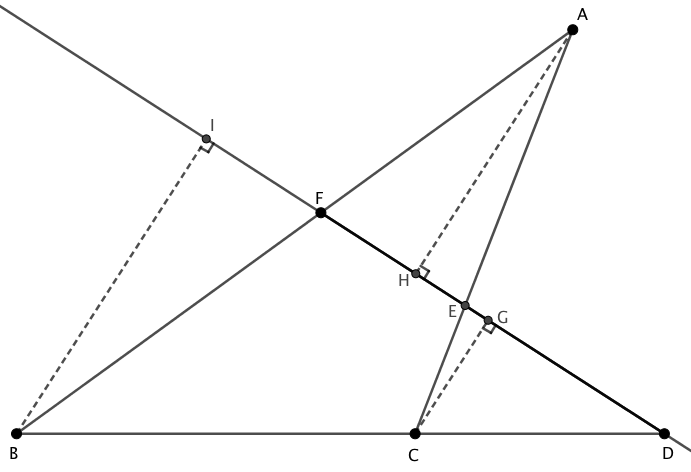
メネラウスの定理の証明

△ AFH ∽ △ BFI より、 AF : BF = AH : BI なので、

(1)   \begin{eqnarray*} \cfrac{FB}{AF} = \cfrac{BI}{AH} \end{eqnarray*}

△ DCG ∽ △ DBI より、 DC : DB = CG : BI なので、

(2)   \begin{eqnarray*} \cfrac{DC}{BD} = \cfrac{CG}{BI} \end{eqnarray*}

△ EAH ∽ △ ECG より、 EA : EC = AH : CG なので、

(3)   \begin{eqnarray*} \cfrac{EA}{CE} = \cfrac{AH}{CG} \end{eqnarray*}

(1), (2), (3)式の各辺をそれぞれかけ合わせると

    \begin{eqnarray*} \cfrac{FB}{AF} \cdot \cfrac{DC}{BD} \cdot \cfrac{EA}{CE} &=& \cfrac{BI}{AH} \cdot \cfrac{CG}{BI} \cdot \cfrac{AH}{CG} \\\\ &=& 1 \end{eqnarray*}

以上により、

    \begin{eqnarray*} \cfrac{FB}{AF} \cdot \cfrac{DC}{BD} \cdot \cfrac{EA}{CE} &=& 1 \\\\ \end{eqnarray*}

が証明されました。

メネラウスの定理の覚え方

三角形の頂点の名前は問題によって異なりますので、メネラウスの定理をそのまま記号として丸暗記してもうまく使えないことがあります。

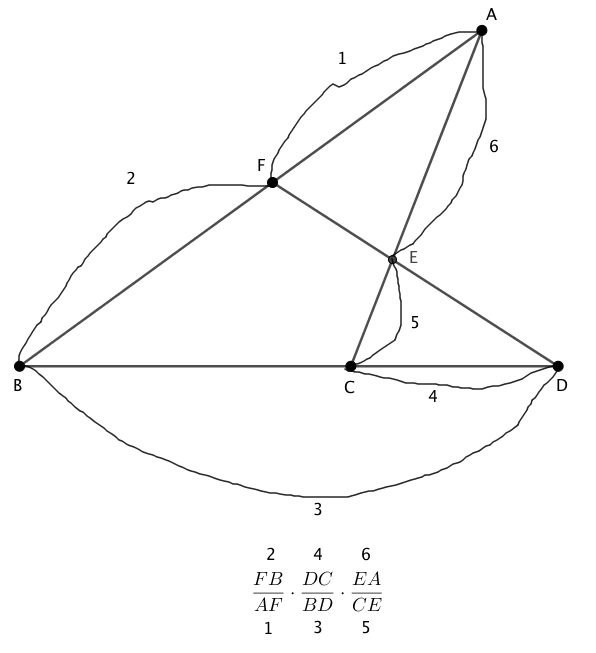
下の図のように、適当に頂点を選び（この場合はA）、ぐるっと1周回るというように覚えておきましょう。

メネラウスの定理の覚え方

よくある間違いとして、次のように誤った式を立ててしまうことがあるかもしれません。

    \begin{eqnarray*} \cfrac{FB}{AF} \cdot \cfrac{CD}{BC} \cdot \cfrac{EF}{DE} &=& 1 \\\\ \end{eqnarray*}

この場合は A から始まって F で終わってしまっているので、うまくぐるっと1周できていないことになります。

開始と終了の点は一致していなければなりませんので、開始点にうまく戻ってこれるように三角形を1周しましょう。

考え方としては、対象としている三角形の頂点とそれ以外の点を交互に経由すれば良いと言えます。

本例では三角形 ABC を対象としていますので、

A → ? → B → ? → C → ? → A

という具合になります。

上の?の部分にはそれぞれ直線 AB, BC, CA 上の点つまりF, D, E を入れます。すると、

A → F → B → D → C → E → A

という順番になり、これをしりとりのように組み合わせると

AF, FB, BD, DC, CE, EA となります。

そしてこれを順に分数にしていくと

    \begin{eqnarray*} \cfrac{FB}{AF} \cdot \cfrac{DC}{BD} \cdot \cfrac{EA}{CE} \end{eqnarray*}

という正しい式を作ることができます。

メネラウスの定理の説明のおわりに

いかがでしたか？

メネラウスの定理はチェバの定理より図形が難しいぶん、少しとっつきにくく感じられるかもしれません。

しかし、覚え方のところでも述べたとおり「三角形の頂点とそれ以外の点を交互に経由する」と理解すれば、チェバの定理もメネラウスの定理も使い方（式の立て方）としては同じになります。

定理を式として暗記するのではなく、図形と関連させ、どのように立式すれば良いかという観点で理解しておくようにしましょう。

【基礎】図形の性質のまとめ

公式

図形の性質

プロフィール

-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。

検索

この記事の目次

関連記事

サイドメニュー