勉強の前に

数学を勉強していると新しい公式が次から次へと登場してきますが、「こんなに覚えられるわけない！」と思ったことはありませんか？

一部の特殊な力を持つ方以外の方（私も含めほとんどの方が特殊な力は持っていません）は、そう簡単にものを覚えることはできないのです。

では一体どうしたらいいのでしょうか？

その答えは簡単です。公式は覚えずに作ればいいのです。

公式を作る過程では証明という手段が必要になりますので、公式とその証明は切っても切り離すことができないものになります。

今回は数学の公式との正しい付き合い方についてお話ししていきたいと思います。

マジックナンバーを超える情報量は一度に処理できない

心理学用語で「マジックナンバー」という言葉があります。
これは「人間が瞬間的に記憶できる短期記憶の限界数」のことで、現在の研究によるとマジックナンバーは「4」だそうです。

つまり、数学の勉強中で言うならば、一度に4つ以上の公式が出てきたら覚えられないということになります。

とはいっても、「瞬間的」に記憶できる情報量には限界があるということにすぎませんので、ゆっくり時間をかけて一つ一つ覚えていけば良いということも言えるでしょう。
しかし、私はその方法はあまり得策ではないと思っています。

ではどうすればよいのでしょう？

12345678と99875279のどちらが覚えやすいですか？

例えば、8桁の数字を瞬間的に覚えなければならない場合、12345678と99875279のどちらが覚えやすいですか？

12345678については、規則的に1ずつ増えていく8桁の数であることは瞬間的にでもわかるでしょう。
最初の数が1であることと、1ずつ増えることを覚えれば、最初の数以降は覚える必要すらありません。

一方99875279はどうでしょうか？
簡単には規則性は見当たらず、意味はわからないがとにかく覚えるという方法をとることになります。

断然、12345678のほうが覚えやすいですよね？
しかも一瞬で8桁もの数を覚えられていることになるので、12345678を記憶することは、マジックナンバーの制限にかからないことになります。これは規則性という意味づけによるものです。

多くの場合、瞬間的に記憶するという状況において、記憶しなければならない対象に意味を見いだす時間はありません。

99875279のように、なんだか分からないがとにかく覚える、というのは相当にハードルが高くなるのです。

しかしこの例の場合は、12345678という極端に覚えやすい数字を例にしたからマジックナンバーの制限がかかっていないだけです。

99875279についてはマジックナンバーの制限がかかっています。
どうすれば良いでしょうか？

マジックナンバーの制限から逃れましょう

先の例で12345678と99875279を暗記する場合、規則性により12345678の方が覚えやすいというお話しをしました。

しかし、実は99875279にも規則性があり、次の規則に従っています。 規則 

1. 最高位の数とその一つ下の位の数を9とする。
2. 連続する二つの位の数の和の1の位の数を、その一つ下の位の数とする。

実際にこの規則で位の高い方から順に数字を並べていくと、次のようになります。

9（規則1より、9）
99(規則1より、9）
998(規則2より、9+9=18 → 8)
9987(規則2より、9+8=17 → 7)
99875(規則2より、8+7=15 → 5)
998752(規則2より、7+5=12 → 2)
9987527(規則2より、5+2=7 → 7)
99875279(規則2より、2+7=9 → 9)

99875279という数字の並びを「作る」ことができました。

ここで気になることがあります。
それは、99875279を「覚え」なければならなかったのに、「作って」しまったことです。

しかし、「覚えた」99875279と、「作った」99875279に、どのような違いがあるでしょうか？
どちらも得られる結果はただの99875279ですので、違いはありません。

8桁の数字を「作れた」のなら8桁の数字を「覚えた」のと同じであり、つまりそれは「作る」ことによってマジックナンバーの制限から逃れられるということを意味しています。

でも「作る」には規則を知っている必要がありますよね？
99875279という数字を眺めただけでは、到底規則性に気づくことなどできません。

数学の公式も同じで、眺めているだけではよくわからないのです。
さらに、公式に規則性というものが存在しているかどうかも定かではありません。

よって、規則性に限らず、公式を覚えるにはなんらかの意味付けを行うとよいという観点で話を進めていきましょう。

語呂合わせで意味付ける

の近似値を覚えていますか？
ですね？

覚えている方は、「富士山麓オウム鳴く（ふじさんろくおーむなく）」と覚えたはずです。
そして、頭の中で「覚えた」富士山麓オウム鳴くを唱えながら、という数字を「作る」のです。

無理数の近似値には規則性はありませんので、語呂合わせを用いて意味付けを行っているわけですね。

「にーてんにーさんろくれいろくななきゅう」と覚えている方はごくまれでしょうし、この覚え方ではすぐに忘れたり間違えたりしてしまいそうです。

「富士山麓オウム鳴く」ならそれ自体に意味はありますから、覚えやすく、忘れにくく、間違えにくいといえるでしょう。
つまり、人間が何かを覚えるには、それに意味があった方が覚えやすいということですね。

しかし、全ての公式でうまい具合に語呂合わせができるわけではないので、語呂合わせは万能な方法ではないと言えるでしょう。

さらに、語呂合わせには致命的な欠点があります。それは、その語呂でなければならない理由がないことです。

「富士山麓オウム鳴く」は、「富士山麓にオウム鳴く」としても、日本語の意味自体は変わりません。しかし「に」がついてしまったら、実際とは異なったの近似値を答えてしまうことになるでしょう。

「富士山麓オウム鳴く」でならなければならない理由がないのですね。

ではどうしたら良いのでしょうか？

公式の意味自体を覚えよう

公式の意味とは何か。それは公式自体を見てもわかりません。
なぜなら、公式自体は「結果」だからです。

ラマヌジャンが作る式を他人が理解するには少なくとも100年かかります。

次の式を見て下さい。

   

全く意味がわかりませんよね？

これはラマヌジャンという数学者が発表した円周率を求めるための公式です。

ラマヌジャンは「証明」という概念を持っておらず、証明の添えられていない公式をノートに残し、その生涯を終えてしまいました。

ラマヌジャンの死後、世界中の優秀な学者がこの式の証明を試みるのですが、解決には100年を要しました。

少し極端な例だったかと思いますが、いかに結果だけを見ても意味はわからないということがおわかりいただけたかと思います。

公式の結果だけを見ることは、映画のクライマックスシーンだけを見ることと同じである。

映画のクライマックスシーンだけを見ても、なぜそのようになったのか意味もわからず、腑に落ちず、感動することも出来ませんよね？
映画ではどこに重要な要素が隠れているかわかりませんから、最初から見るに越したことはありません。

映画と同様に、公式についても最初から見ていくべきなのです。
公式の最初とはどこでしょうか？
それはその公式の証明部分にあたります。
公式の意味はその公式の証明の中にあるのです。

語呂合わせの致命的な欠点である「理由がない」ことに対して、証明には必ず理由があります。
むしろ、理由だけで構成されていると言ってもいいでしょう。

理由がわかれば、その理由自体を公式に意味付けて覚えてしまえば良いのです。

だから証明をよく読みましょう。そして自分で証明できるようにしてください。

証明の実例を見てみましょう

ここでは三角比（三角関数）を題材としましょう。

三角比に関する公式はとても多く、しかも覚えにくいという特徴があります。

公式数が多くなるのは全ての公式が, , の三種類について存在するからで、覚えにくいのはそれぞれの式が少しだけ違うからです。

公式をいくつかあげてみましょう。

-θの三角比

   

180°-θの三角比

   

それぞれの公式が3つの式で構成されており、二つの公式を紹介しただけで式は6つも出てきてしまいました。
そして、二種の公式では右辺は符号がつくかつかないかだけの違いであり、とても覚えにくいですね。

それでは、証明を見てみましょう。

-θの三角比の証明

次の図のような単位円を考えましょう。

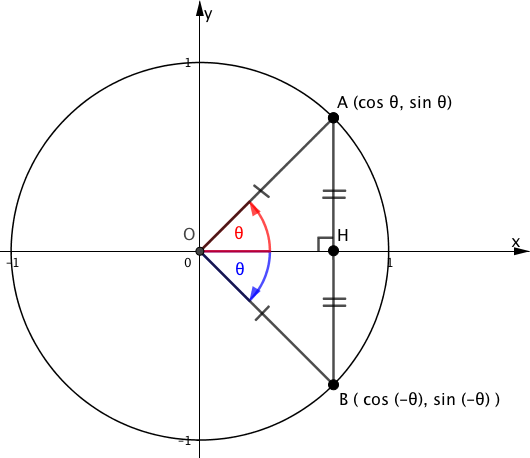
動径の正の向きは反時計回りと一般的に決められているので、青色のはを意味しています。
よって、点Bの座標はとなります。
また、辺OHはの二等分線であり、△は二等辺三角形なので、「二等辺三角形の頂角の二等分線は底辺を垂直に二等分する」ことにより、

   

となります。

よって、△と△はx軸に関して対象な図形となり、

   

であることが証明されました。

上の結果と、より、

   

よって、

   

であることが証明されました。

180°-θの三角比の証明

公式を再掲します。

   

この公式の証明を行っていきます。

次の図のような単位円を考えましょう。

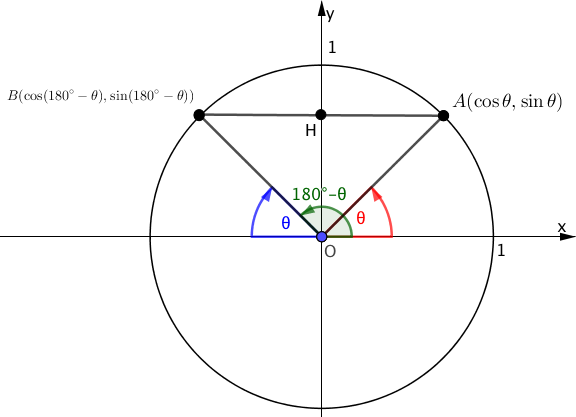
の三角比で証明した内容と同様にして、△と△はy軸に関して対象な図形となります。

これにより、

   

が証明されます。

上の結果と、より、

   

よって、

   

であることが証明されました。

証明を読んだ後に感じて欲しいこと

証明を読んでみてどのように感じたでしょうか？

難しく感じた、簡単に感じた、意味がわからなかった、など様々なものがあるかと思います。

しかし証明内容について深く論じるつもりはありません。
私が皆さんに感じてもらいたいことは、証明さえできれば公式を覚えていなくてもいいということです。証明をすれば公式は作れるのですから。

つまり、公式は覚えるものでなく、作るものなのです。

また、証明の中で使われている事柄で、知らないことはありましたか？
全て既存の知識を使って証明が行われていますよね？
つまり、新しい公式は既に知っていることだけが使われて出来ているのです。

そして、の公式の証明については、「同様に」という言葉で証明が済んでいます。
「同様に」すれば良いのですから、の公式が証明できれば、の公式の証明もできるわけです。
これはつまり、ある公式の証明は他の公式の証明に利用できるということです。

単純暗記なら6つの式を意味もなく覚えることになりますが、証明から理解することができれば一つ目の公式の証明方法たった1つだけを覚えればよいことになります。

そして、実際に証明をすることにより、公式は無意味な数値の羅列のようなものでなくなります。
証明自体が意味なのですから。

人間が何かを覚えるには、それに意味があった方が覚えやすいという話をしましたが、意味がない6つと、意味がある1つのどちらが覚えやすいですか？
答えは明白ですね。

そもそも覚えていなければ忘れることがない

公式の導出が出来ない場合は、意味を考えずに単純に公式を覚えるしかありません。
そして、覚えたことはいつか忘れます。間違えることもあります。
人間の記憶というのはあいまいなものですから、これを避けることはできません。

公式を証明し自ら導出するという過程を経るようにすれば、記憶に頼る部分が少なくなります。
覚えておかなければならないのは証明の方法だけです。

証明の内容は理論に基づいているものですので、人間のあいまいな記憶が介入することがないのです。そして正しい理論を元に得られた結果が否定される要因などありません。
証明に頼れば、忘れることもないし、間違えることもないのです。

さて、覚えたことは忘れてしまうのですが、それならどうすればよいですか？

答えは、覚えなければいいということになります。

自信をもって回答するためには証明の練習が不可欠

証明を行うと、数学の能力は飛躍的に向上します。
無意味な結果（単純暗記した公式）をこねくり回していると、やってはいけいないこと（適切でない公式の使い方）をやってしまうことがよくあります。
しかし、意味から（証明から）理解した公式についてはそのようなことは起きません。
その公式が成立する条件などの周辺的な事柄は証明内に含まれており、その全てを理解できているからです。

さらに、数学においては常に、なぜそうなったかが重要です。
マークシート方式の試験ならば答えに至る過程を説明する必要はなく、回答欄を埋めていくだけで回答は作れてしまいます。
しかし、そこに埋めた数字は何らかの計算を行なった結果得られたものですよね？
その数字は本当に正しいですか？自信をもってその回答を書くことができますか？

不安になりますよね？

その答えが正しいという理由を自分自身で見いだせれば、自信をもって回答することができるはずです。
そのために、なぜそうなったかを突き詰めることが重要なのです。

なぜそうなるかを示すためのものが証明なのですから、証明は「なぜ？」を突き詰める最適な練習台になるのです。

その公式の証明ができるのであれば、その公式は覚えておいた方が良い

さて、ここまでさんざん公式は覚えなくていいということを主張してきましたが、実際には公式は覚えていた方がいいです。

公式を覚えなくていいというのは、証明すればその公式が作れるからです。
ということは公式を覚えていない場合は、毎回証明しなければならないということになってしまうのです。

試験には時間という制約がありますから、素早く問題を解いていかなければなりません。
そんな状況のときに、いちいち証明を行うことは決して得策ではないのです。

実際に問題を解くときにはその公式の証明を使うのではなく、その公式の結果を使います。
つまり公式は道具なわけです。

道具はいつでもすぐに使えるような状態である方が良いですよね？
その意味では、公式は覚えている方が良いことになります。

公式は道具だと言いましたが、道具を適切に使うためには説明書を読まなければなりませんね？
この場合の説明書とは、その公式の証明の内容にあたります。
だから、証明内容自体をも把握しておく必要があります。しかし説明書は一度読めばわかりますよね？だから毎回証明する必要はないのです。

公式は覚えている方が良いのですが、覚えたことは忘れるという話もしましたね？
公式を忘れた時のために、公式の導出方法を覚えておくということが万一のときのための保険として機能するのです。

公式の導出ができるというのは、その公式について深く理解できているということになりますので、それはプラスに働きます。そのうえで、素早く道具を使うためには公式を覚えていた方がいいのです。

つまり、その公式について証明できるし、公式の形も丸暗記していることが理想だということです。

すべての公式は覚えておいた方が良いが、証明の力をつけるためには公式は覚えていない方がいい

公式の証明ができることは、公式を覚えているいないに関わらず必須なのですが、
証明はそれ自体が道具ではないから、おろそかにされがちです。
しかし、証明は「なぜ？」を追求する練習に最適だというお話もしました。

「なぜ？」の追求は数学の根本ですので、絶対に証明の練習を欠かしてはいけません。

だからまずは公式を覚えないようにしましょう。

公式を覚えていなければ証明して自分で公式を作るしかないので、公式を覚えていないことにより必然的に証明の練習が行われるわけです。

その結果、証明の能力が上がり、「なぜ？」の追求ができるようになるのです。

そして、証明を繰り返せば嫌でも公式は単純暗記できます。

公式を覚えていれば、問題を解く方針を決めることができる

たとえば、三平方の定理 を暗記しているものとします。
このとき と がわかっている状況ならば、 を求めることが可能であり、 がわかることで問題の解決に結びつくのであれば、 を求めればよいという方針を決定することができます。

しかし、もしも三平方の定理を暗記していない場合は、を求めることは不可能であると判断してしまいかねない状況にあります。

たとえ がわかれば問題の解決に結びつくと判断できたとしても、それを求める術がないので、問題を解き進めることができないといったことになってしまうかもしれません。

このように公式を覚えているということは、公式を使って計算を行うことができるということだけでなく、問題を解き進める方針を決定することができるという側面で、非常に重要な意味を持ちます。

基本的な公式の存在自体を知らなければ、問題を解く方針決定ができない、つまりわからない、という状況になります。

この状況は数学が苦手だと感じている方ほど陥りやすいと思われます。
問題を解くための方針決定の補助の意味合いとして、公式を覚えましょう。

三平方の定理の場合は、「直角三角形の二辺の長さがわかっていれば、三辺目の長さを求めることは可能である」ということ自体を覚えることが重要です。それさえ覚えていれば全く問題がわからないという状況を防ぐことはできます。

三平方の定理は直角三角形の三辺を変数とした定理ですので、二つの変数の値がわかれば最後の一つの変数の値がわかるということを、定理自体が物語っています。

公式を見ればその公式はどんなときに有用であるかまで判断することができますので、公式自体だけでなくその使い所まで意識して公式を覚えると良いでしょう。

覚えていることの価値は時代と共に下がり続けています

インターネットで調べれば多くのことがわかる時代になってしまいましたので、何かを覚えていることに対する価値はどんどん下がり続けています。

といっても、最低限のことは覚えていなければなりません。
「最低限のことって何？」と思われるかもしれませんが、最低限のボーダーラインは私もわかりません。個々人の置かれた状況によっても変わるでしょう。

少なくとも、私は「覚えていなくてもわかることは、覚えなくてよい」と考えています。
そして、覚えていなくてもわかるようなことの範囲を増やすことで、インターネット上にも存在していないような問題の答えを見つけることができるようになるでしょう。

覚えていないことや知らないことにいかに対応できるかが、これからの時代を強く生き抜くためのヒントになるかもしれませんね。

追記

覚えておかなければならない対象というのは、そのときどきによって変わることがあります。

覚えておくべきことは何か、今それを覚える必要があるのか、などといった数学と暗記にまつわる様々を習熟度別にまとめましたので、これについては下の記事をご覧ください。

正しい暗記数学の方法と暗記数学の限界