公式

今まで学んだ展開公式として、中学数学で学んだ

$$\begin{array}{rcl} (x + y)^2 &=& x^2 + 2 xy + y^2 \\\\ \end{array}$$

や、三乗の展開公式で学んだ

$$\begin{array}{rcl} (x + y)^3 &=& x^3 + 3 x^2 y + 3 x y^2 + y^3 \\\\ \end{array}$$

といったものがあります。

次に問題となるのが、 $(x + y)^4$ や $(x + y)^5$ ですが、数字を一つずつ増やして調べていくのではきりがありませんね？

ここでは $n$ 乗の展開、つまり $(x + y)^n$ を計算するための方法である、二項定理についての解説を行っていきます。

二項定理とは

二項定理とは次の式のことをいいます。

二項定理の証明

二項定理の証明 (n=3のとき)

$ (x_1+y_1)(x_2+y_2)(x_3+y_3) $
$= (x_1x_2 + x_1y_2 + y_1x_2 + y_1y_2)(x_3+y_3) $
$= x_1x_2x_3+ x_1x_2y_3 + x_1y_2x_3 + x_1y_2y_3 + y_1x_2x_3 + y_1x_2y_3 + y_1y_2x_3 + y_1y_2y_3$

$(x + y)^3$ を累乗を使わずに書き下すと次のようになります。

$$\begin{array}{rcl} (x + y)^3 &=& (x + y)(x + y)(x + y) \\\\ \end{array}$$

xを3個選ぶ場合

3つあるかっこのうちから3つとも $x$ を選ぶことになりますので、 それらの積により $x^3y^0$ が作られますが、その選び方は ${}_3 \mathrm{C} _{3}$ 通りであることから ${}_3 \mathrm{C} _{3}$ 個の $x^3y^0$ が作られます。
これにより計算結果は ${}_3 \mathrm{C} _{3} x^3y^0 $ となります。

xを2個選ぶ場合

3つあるかっこのうちから2つの $x$ を選ぶことになりますので、 それらの積により $x^2y^1$ が作られますが、その選び方は ${}_3 \mathrm{C}_ {2}$ 通りであることから ${}_3 \mathrm{C} _{2}$ 個の $x^2y^1$ が作られます。
これにより計算結果は ${}_3 \mathrm{C} _{2} x^2y^1 $ となります。

xを1個選ぶ場合

3つあるかっこのうちから1つの $x$ を選ぶことになりますので、 それらの積により $x^1y^2$ が作られますが、その選び方は ${}_3 \mathrm{C} _{1}$ 通りであることから ${}_3 \mathrm{C} _{1}$ 個の $x^1y^2$ が作られます。
これにより計算結果は ${}_3 \mathrm{C} _{1} x^1y^2 $ となります。

xを0個選ぶ場合

3つあるかっこのうちから $x$ を選ばないので、それはつまり3つとも $y$ を選ぶことを意味します。よって、それらの積により $x^0y^3$ が作られますが、その選び方は ${}_3 \mathrm{C} _{0}$ 通りであることから ${}_3 \mathrm{C} _{0}$ 個の $x^0y^3$ が作られます。
これにより計算結果は ${}_3 \mathrm{C} _{0} x^0y^3 $ となります。

これらをまとめると

以上により、

$(x + y)^3 = {}_3\mathrm{C}_3x^3y^0 + {}_3\mathrm{C}_2x^2y^1 + {}_3\mathrm{C}_1x^1y^2 + {}_3\mathrm{C}_0x^0y^3$

であり、これを整理すると

$$\begin{array}{rcl} (x + y)^3 &=& x^3 + 3 x^2y + 3 xy^2 + y^3\\\\ \end{array}$$

となり、3乗の展開公式の結果に一致し、 $n=3$ のときに二項定理が成立することが示されました。

同様にして、一般の $n$ の場合についても考えてみましょう。

二項定理の証明 (一般のnのとき)

$(x + y)^n$ を $n$ 個の $(x + y)$ の積の形に書き下すと次のようになります。

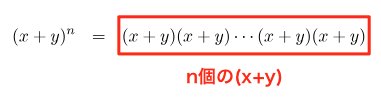
この $n$ 個の $(x + y)$ のそれぞれのかっこから $x$ または $y$ を選択することによって展開結果を考えましょう。

xをn個選ぶ場合

$n$ 個のかっこのうちから $n$ 個とも $x$ を選ぶことになりますので、 それらの積により $x^ny^0$ が作られますが、その選び方は ${}_n \mathrm{C} _{n}$ 通りであることから ${}_n \mathrm{C} _{n}$ 個の $x^ny^0$ が作られます。
これにより計算結果は ${}_n \mathrm{C} _{n} x^ny^0 $ となります。

xをn-1個選ぶ場合

$n$ 個のかっこのうちから $n-1$ 個の $x$ を選ぶことになりますので、 それらの積により $x^{n-1}y^1$ が作られますが、その選び方は ${}_n \mathrm{C} _{n-1}$ 通りであることから ${}_n \mathrm{C} _{n-1}$ 個の $x^{n-1}y^1$ が作られます。
これにより計算結果は ${}_n \mathrm{C} _{n-1} x^{n-1}y^1 $ となります。

xをr個選ぶ場合

$n$ 個のかっこのうちから $r$ 個の $x$ を選ぶことになりますので、 それらの積により $x^{r}y^{n-r}$ が作られますが、その選び方は ${}_n \mathrm{C} _{r}$ 通りであることから ${}_n \mathrm{C} _{r}$ 個の $x^{r}y^{n-r}$ が作られます。
これにより計算結果は ${}_n \mathrm{C} _{r} x^{r}y^{n-r} $ となります。

xを1個選ぶ場合

$n$ 個のかっこのうちから $1$ 個の $x$ を選ぶことになりますので、 それらの積により $x^{1}y^{n-1}$ が作られますが、その選び方は ${}_n \mathrm{C} _{1}$ 通りであることから ${}_n \mathrm{C} _{1}$ 個の $x^{1}y^{n-1}$ が作られます。
これにより計算結果は ${}_n \mathrm{C} _{1} x^{1}y^{n-1} $ となります。

xを0個選ぶ場合

$n$ 個のかっこのうちから $0$ 個の $x$ を選ぶことになりますので、 それらの積により $x^{0}y^{n-0}$ が作られますが、その選び方は ${}_n \mathrm{C} _{0}$ 通りであることから ${}_n \mathrm{C} _{0}$ 個の $x^{0}y^{n-0}$ が作られます。
これにより計算結果は ${}_n \mathrm{C} _{0} x^{0}y^{n-0} $ となります。

これらをまとめると

以上により、

$ (x + y)^n = {}_n\mathrm{C}_n~x^{n} y^{0} + {}_n\mathrm{C}_{n-1}~x^{n-1} y^{1} + \cdots + {}_n\mathrm{C}_{r}~x^{n-r} y^{r} + \cdots + {}_n\mathrm{C}_{1}~x^{1} y^{n-1} + {}_n\mathrm{C}_{0}~x^{0} y^{n-0}\\$

となります。ここで組み合わせの性質から、

$$\begin{array}{rcl} {}_n \mathrm{C} _{m} = {}_n \mathrm{C} _{n-m} \end{array}$$

が成り立つので、

$ (x + y)^n = {}_n\mathrm{C}_0~x^{n} y^{0} + {}_n\mathrm{C}_1~x^{n-1} y^{1} + \cdots + {}_n\mathrm{C}_r~x^{n-r} y^{r} + \cdots + {}_n\mathrm{C}_{n-1}~x^{1} y^{n-1} + \cdots + {}_n\mathrm{C}_{n}~x^{0} y^{n-0} \\$

となります。

以上により、一般の $n$ のときに二項定理

が成立することが示されました。

二項定理の説明のおわりに

いかがでしたか？

展開結果の係数は組み合わせを用いて説明できるということについて、意外に感じられた方も多くおられるかと思います。

また、一般の $n$ についての証明で $x$を $r$ 個選ぶ場合を考えましたが、そのときの計算結果である

$$\begin{array}{rcl} {}_n \mathrm{C} _{r} ~x^{r}y^{n-r} \end{array}$$

を一般項といい、一般項とは一般に第 $n$ 番目の項のことを意味しますのでこのことも覚えておきましょう。

一般項については数列を学ぶと身近に感じられるようになるかと思います。

【基礎】方程式・式と証明のまとめ