学校や塾では教えてくれない、元塾講師の思考回路の公開

解法

【東大の入試問題を解説！】2018年度入試 東京大学 前期日程 数学（理科） 第1問

今回は東京大学の入試問題を扱います。

東大の問題と聞くと身構えてしまうかもしれませんが、国立大学の問題は教科書に載っている知識のみで解けるように作られています。
順序立てて進めていくことで解決していきましょう。

それでは問題を見てみます。

2018年度入試 東京大学 前期日程 数学（理科） 第1問

2018年度入試 東京大学 前期日程 数学（理科） 第1問

マスマスターの思考回路

「増減表をつくり」とあるので他のことは考えず、とりあえず微分しましょう。

商の微分と三角関数の微分を用いて計算を行いましょう。

    \begin{eqnarray*}f'(x) &=& \cfrac{\sin x - x\cos x}{\sin^{2} x} - \sin x \\\\&=& \cfrac{\sin x - x\cos x - \sin^3 x}{\sin^2 x} \\\\&=& \cfrac{\sin x (1 - \sin^2 x)- x\cos x}{\sin^2 x} \\\\&=& \cfrac{\sin x (\cos^2 x)- x\cos x}{\sin^2 x} \\\\&=& \cfrac{\cos x　(\sin x \cos x- x)}{\sin^2 x} \\\\\end{eqnarray*}

マスマスターの思考回路

0 < x < \pi　における　\cos x の符号は明確ですが、 \sin x \cos x- x の符号は簡単にはわかりません。次の図を利用しましょう。

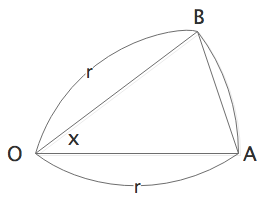
sin xと xの大小関係

上図から、三角形OABの面積 < 扇型OABの面積となるので、

    \begin{eqnarray*} \cfrac{r^2 \sin x}{2} < \cfrac{r^2 x}{2} \end{eqnarray*}

つまり、

    \begin{eqnarray*} \sin x < x \end{eqnarray*}

が成り立ちます。

また、0 < x < \pi のとき、-1 < \cos x < 1なので、

    \begin{eqnarray*} \sin x \cos x < x \end{eqnarray*}

よって、

    \begin{eqnarray*} \sin x \cos x- x < 0 \end{eqnarray*}

となります。

マスマスターの思考回路

0 < x < \pi における \sin x と x の大小関係が \sin x < x であることを知っていると、この解法を思いつくことができます。
\sin x < x であり、 -1 < \cos x < 1 であることから \sin x \cos x- x < 0　が成立することを事前に確認した上で、この解法を選択しています。
\sin x < x を証明なしで使うことははばかられるので、図を添えて証明しています。
上図は三角関数の極限の証明に使用される図なので、覚えておきましょう。

以上から増減表は次のようになります。

    \begin{eqnarray*}\begin{array}{c||c|c|c|c|c}\hline x&0&\cdots&\frac{\pi}{2}&\cdots&\pi\\\hline f'(x)&&-&0&+&\\\hline f(x)&&\searrow&\frac{\pi}{2}&\nearrow&\\\hline\end{array}\end{eqnarray*}

また、極限は

    \begin{eqnarray*}\displaystyle　\lim_{x \to +0} \frac{x}{\sin　x} + \cos x &=& 1 + 1 \\\\&=& 2\end{eqnarray*}

    \begin{eqnarray*}\displaystyle　\lim_{x \to \pi - 0} \frac{x}{\sin　x} + \cos x &=& +\infty - 1 \\\\&=& +\infty\end{eqnarray*}

となります。

この記事が気に入ったら
「いいね」しよう！

解法

極限 微分

プロフィール

-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。

検索

この記事の目次

関連記事

サイドメニュー