学校や塾では教えてくれない、元塾講師の思考回路の公開

公式

【公式】関数の対称移動について解説するよ

今回は関数のグラフの対称移動についてお話ししていきます。

対称移動は平行移動とともに、グラフの概形を考えるうえで重要な知識となりますのでしっかり理解しておきましょう。

【公式】関数の平行移動について解説するよ



ここでは y &=& 2x^2 - 3x + 1 という関数を例として、対称移動の具体例をみていきましょう。

x軸に関する関数の対称移動

下の図のように、黒色の関数を x 軸に関して対称移動した関数が赤色の関数となります。

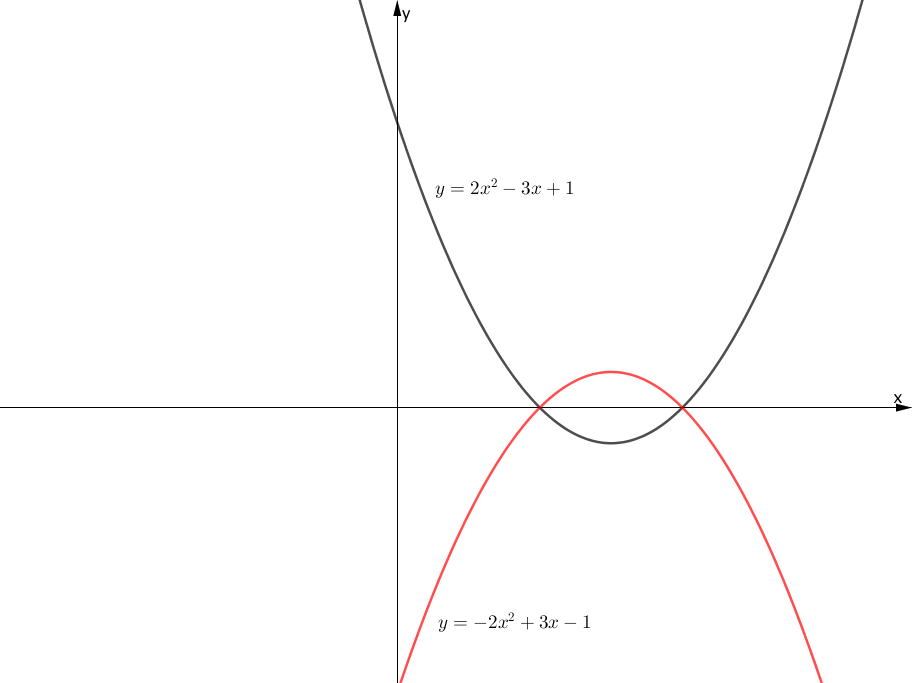
x軸に関する関数の対称移動

対称移動前後の関数を比較するとそれぞれ、

    \begin{eqnarray*} y &=& 2x^2 - 3x + 1 \end{eqnarray*}

    \begin{eqnarray*} y &=& -2x^2 + 3x - 1 \end{eqnarray*}

であり、右辺の符号が真逆の関数となっていますが、なぜこのようになるのでしょうか？

まず、 x 軸に関して対称に移動するということは、 y 座標の符号を変えるということと同じです。

例えば、点 (2, 3) を x 軸に関して対称に移動すると、その座標は (2, -3) となりますね？

それをもとの関数上の全ての点について行うと、関数全体が x 軸に関して対称に移動されたことになるというわけです。

計算上は下のように y &=& 2x^2 - 3x + 1 という関数の y を -y に置き換えることにより、 x 軸に関して対称に移動した関数を求めることができます。

    \begin{eqnarray*} -y &=& 2x^2 - 3x + 1 \\\\ y &=& -2x^2 + 3x - 1 \\\\ \end{eqnarray*}

一般に、次のことが成り立ちます。

y = f(x) を x 軸に関して対称に移動した関数は、

    \begin{eqnarray*} y = -f(x) \end{eqnarray*}

により求められる。

y軸に関する関数の対称移動

下の図のように、黒色の関数を y 軸に関して対称移動した関数が赤色の関数となります。

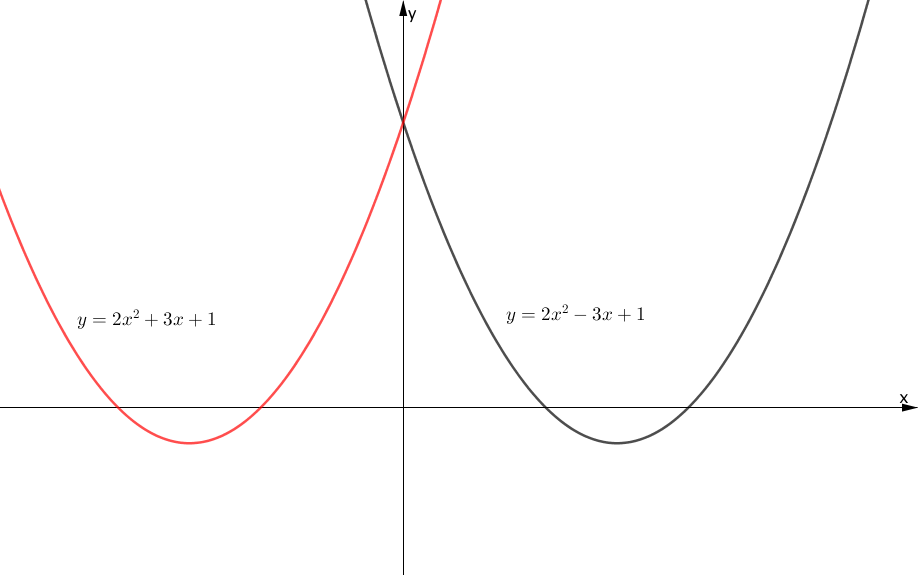
y軸に関する関数の対称移動

対称移動前後の関数を比較するとそれぞれ、

    \begin{eqnarray*} y &=& 2x^2 - 3x + 1 \end{eqnarray*}

    \begin{eqnarray*} y &=& 2x^2 + 3x + 1 \end{eqnarray*}

であり、 x の項の符号のみが変わっていますね。

x 軸に関する対称移動と同様に考えて、 y 軸に関する対称移動は、関数上の全ての点の x を -x に置き換えることにより求められます。

計算は次のようになります。

    \begin{eqnarray*} y &=& 2(-x)^2 - 3(-x) + 1 \\\\ &=& 2x^2 + 3x + 1 \\\\ \end{eqnarray*}

一般に、次のことが成り立ちます。

y = f(x) を y 軸に関して対称に移動した関数は、

    \begin{eqnarray*} y = f(-x) \end{eqnarray*}

により求められる。

原点に関する関数の対称移動

下の図のように、黒色の関数を 原点に関して対称移動した関数が赤色の関数となります。

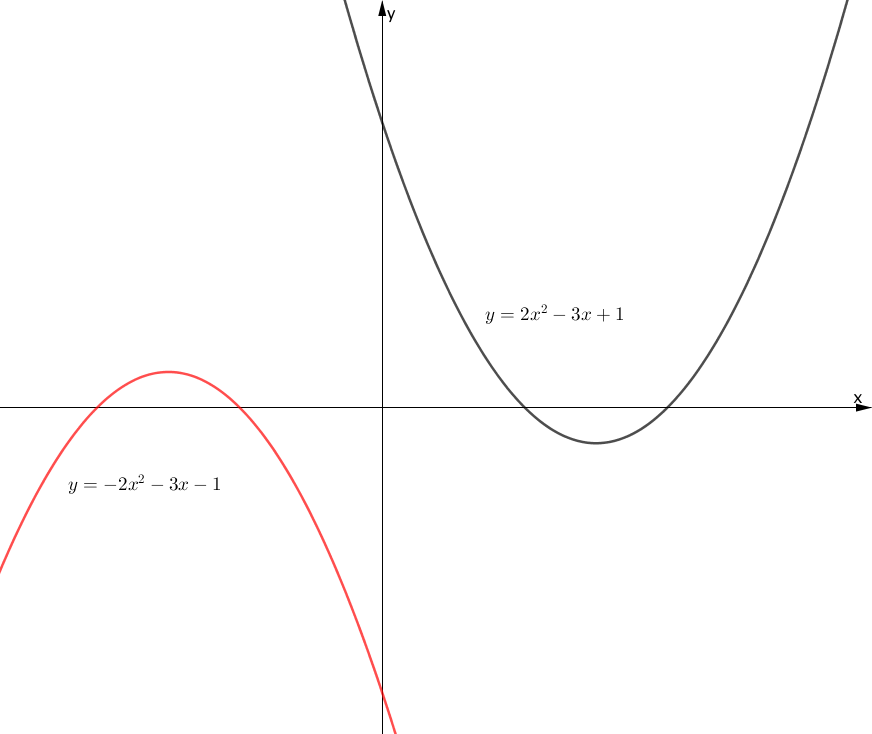
原点に関する関数の対称移動

原点に関する対称移動は、 ここまでの考え方を利用し、関数上の全ての点の x 座標と y 座標をそれぞれ -x, -y に置き換えれば良いですね？

計算は次のようになります。

    \begin{eqnarray*} -y &=& 2(-x)^2 - 3(-x) + 1 \\\\ &=& 2x^2 + 3x + 1 \\\\ y &=& -2x^2 - 3x - 1 \\\\ \end{eqnarray*}

一般に、次のことが成り立ちます。

y = f(x) を原点に関して対称に移動した関数は、

    \begin{eqnarray*} y = -f(-x) \end{eqnarray*}

により求められる。

関数の対称移動についての説明のおわりに

いかがでしたか？

ここでは二次関数を例として対称移動について説明を行いましたが、関数の対称移動は二次関数に限られたものではなく、一般の関数について成り立ちます。

今後様々な関数を学習していくこととなりますが、平行移動・対称移動の考え方がそれらの関数を理解するうえでの基礎となりますので、しっかり学習しておきましょう。

【基礎】二次関数のまとめ

公式

二次関数

プロフィール

-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。

検索

この記事の目次

関連記事

サイドメニュー