学校や塾では教えてくれない、元塾講師の思考回路の公開

公式

【公式】関数の平行移動について解説するよ

今回は平行移動についての解説を行います。
まずは平行移動という言葉の意味を確認しておきましょう。

平行移動とは、「ある点を一定の方向に一定の距離だけ動かすこと」です。

高校数学では関数の平行移動というものを考えます。
関数は無数の点の集まりですから、この無数の点を一律に平行移動させると関数自体も平行移動することになります。

今回は、ある関数を平行移動させた結果、どのような関数になるかを求める方法の説明を行っていきます。

平行移動後の関数の求め方

ある関数 y=f(x) を x 軸方向に p 、 y 軸方向に q だけ平行移動させた関数は、

    \begin{eqnarray*} y-q=f(x-p) \end{eqnarray*}

と表される。

証明

関数y=f(x)上のある点(X, Y)をx軸方向にp、y軸方向にqだけ平行移動させた結果、(x, y)に移動した場合を考えます。

これを図にすると次のようになります。

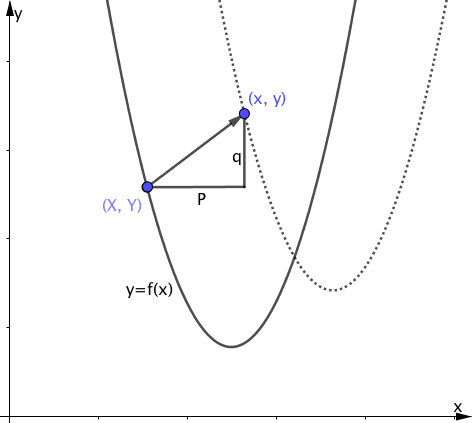
関数の平行移動

y=f(x)上の全ての点について同様に平行移動を行うと、y=f(x)は点線で表された関数に重なるように平行移動されることとなります。つまり、点線部が今求めたい関数です。

点(X, Y)はy=f(x)上にあるので、

(1)   \begin{eqnarray*}Y=f(X) \\\end{eqnarray*}

が成り立ちます。

また、点(X, Y)と(x, y)には次の関係が成り立ちます。

    \begin{eqnarray*}x=X+p \\\\y=Y+q\end{eqnarray*}

これを変形すると、

(2)   \begin{eqnarray*}X=x-p \\\\Y=y-q\end{eqnarray*}

となります。

(2)を(1)に代入すると、

    \begin{eqnarray*} y-q=f(x-p) \end{eqnarray*}

となります。以上により、

ある関数 y=f(x) を x 軸方向に p 、 y 軸方向に q だけ平行移動させた関数は、

    \begin{eqnarray*} y-q=f(x-p) \end{eqnarray*}

と表される。

ことが証明されました。

平行移動の例題

平行移動は数学Iで学習する内容ですが、まだ高校数学に慣れていない高校一年生にとっては、とても難しく感じられる方が多くおられることと思います。

難しいときには具体例を見ることが理解の助けになります。例題を見てみましょう。

例題

y=x^2-2x+3をx軸方向に-4、y軸方向に5だけ平行移動させた関数を求めよ。

解答

マスマスターの思考回路

上で証明した結果は、
y=f(x)をx軸方向にp、y軸方向にqだけ平行移動させた関数はy-q=f(x-p)によって求めることができるということを意味しています。

これは、見方によっては、y=f(x)のyとxをそれぞれy-qとx-pに置き換えるとy-q=f(x-p)になる
と考えることもできますよね？

実際に問題を解くときは常にこの考え方にしたがって解くと良いでしょう。

平行移動後の関数は

    \begin{eqnarray*}y-5=\{x-(-4)\}^2-2\{x-(-4)\}+3 \\\end{eqnarray*}

となります。

これが理解できれば問題は解けたも同然で、あとは式を整理していくだけになります。

    \begin{eqnarray*}y-5&=&\{x-(-4)\}^2-2\{x-(-4)\}+3 \\\\&=&x^2+8x+16-2x-8+3 \\\\&=&x^2+6x+11 \\\\\end{eqnarray*}

左辺の-5を移行すると、

    \begin{eqnarray*}y　&=&x^2+6x+16 \\\end{eqnarray*}

となり、これが平行移動後の関数となります。

関数の平行移動の説明の終わりに

いかがでしたか？

考え方さえ理解できれば、二次関数に限らずどのような関数でも全く同じように平行移動させることができます。
しっかり理解しておきましょう。

【基礎】二次関数のまとめ

公式

二次関数

プロフィール

-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。

検索

この記事の目次

関連記事

サイドメニュー