【基礎知識】乃木坂46の「いつかできるから今日できる」を数学的命題として解釈する
- 命題
基礎知識
基礎知識
ここでは2次関数のグラフと2次不等式について、例題を交えて説明を行います。
2次関数のグラフと2次方程式についての理解が必要となりますので、不安な方はまずそちらを復習しておくと良いでしょう。
2次関数のグラフと2次方程式
2次方程式の「=」が不等号の「<」や「>」となったものを、2次不等式と言います。
例えば、
$$\begin{array}{rcl} x^2-1=0 \end{array}$$は、2次方程式であり、
$$\begin{array}{rcl} x^2-1>0 \end{array}$$は、2次不等式です。
$x^2-3x+2 > 0$ を解け
マスマスターの思考回路

$y=x^2-3x+2$ のグラフは下のようになります。
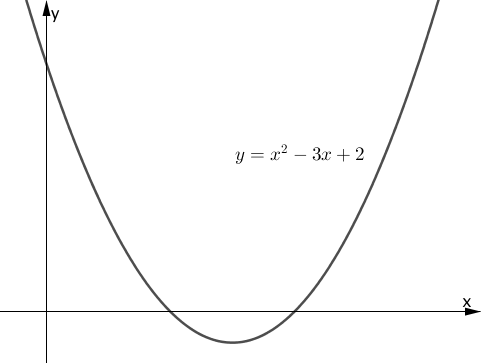
例題の内容は $x^2-3x+2 > 0$ を解くことですが、今、2次関数 $y=x^2-3x+2$ を考えているので、 例題の左辺は $y$ であることになります。
つまり、例題は、
$$\begin{array}{rcl} y > 0 \end{array}$$と同じ意味合いになります。
マスマスターの思考回路

$y > 0$ はそれ自体が不等式の解として問題ない(これ以上計算できない)形となっていますが、例題は $x$ についての2次不等式ですので、 $y > 0$ を答えとすることはできません。
次で、$y > 0$ の意味について考えていきましょう。
$y$ は2次関数の値ですから、 $y > 0$ は2次関数の値が0より大きいということを意味しています。
2次関数の値が0より大きい部分は、下図の赤線で囲んだ部分になります。
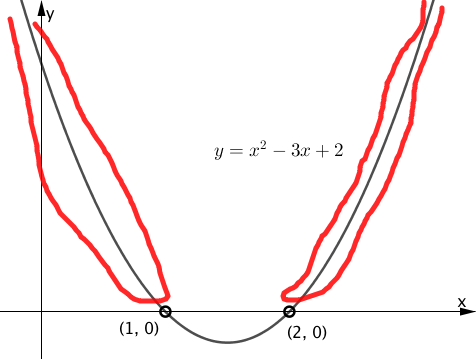
マスマスターの思考回路

$y=x^2-3x+2$ と $x$ 軸との交点の $x$ 座標はそれぞれ 1, 2 となっていますが、これは $x^2-3x+2 = 0$ を解くことによって求められるものです。
上図の赤線で囲んだ部分が、 $y$ でなく $x$ についてどのような位置であるかを考えると、 「$x$ が1より小さい部分または $x$ が2より大きい部分」となります。これを式で表現すればそれが例題の回答であり、下のようになります。
マスマスターの思考回路

例題の解である $x < 1, ~2 < x$ はカンマで区切られていますが、これは二次方程式の解を $x=1, ~2$ のようにカンマで区切って書いていたことと同じ意味合いになります。
つまり、カンマで区切って記述されているものは、それらのうちのいずれもが答えであることを意味すると理解してください。
また、 $x < 1, ~2 < x$ は、 $x < 1, ~x > 2$ と書いても間違いではありませんが、数直線上の大小関係を維持した回答(数直線は一般に右にあるものが大きいので、それに合わせて不等号は $<$ のみを使用する)の方が直感的に理解しやすくおすすめです。
$x^2-3x+2 \leqq 0$ を解け
マスマスターの思考回路

例題2は例題1の不等号が逆向きになり、不等号の下にイコールがついた問題ですが、例題1と同様に考えましょう。
つまり、2次関数の値が0以下になる $x$ の範囲を求めれば良いという問題です。
グラフおよび、解となる範囲(赤線部)は下のようになります。
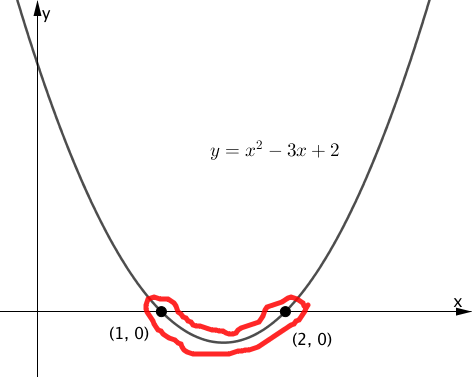
上図より、解は
となります。
マスマスターの思考回路

例題1と異なり、上図では2次関数と $x$ 軸との交点が黒く塗り潰されていますが、これは不等号の下にイコールがついていることを図に表したものです。
例題2は2次関数の値が0以下(つまり0も含む)となる範囲を問われているので、0より大きいか小さいかの境界となる点も解の対象であるという意味になり、その場合は一般に境界となる点が塗りつぶされて描かれます。
ここまでの内容は理解できましたか?
2次不等式を2次関数のグラフと関連づけて解くというのは、基本的な概念の理解という意味合いでは非常に重要ですが、毎回グラフをかくのは手間ですよね?
次に紹介する3つのポイントを理解することで、グラフを描かずに答えを求めることができるようになります。
まず、例題1, 2の問題と回答を再掲します。
例題1 : $x^2-3x+2 > 0$ を解け
回答 : $x < 1, ~2 < x$
例題2 : $x^2-3x+2 \leqq 0$ を解け
回答 : $1 \leqq x \leqq 2$
例題1, 2で、回答に用いられる数値は共通していますね?
つまり、これらは不等号の向きやイコールの有無とは無関係です。
そしてそれらの値は下のように、2次不等式を2次方程式としてみなしたときの解です。
$$\begin{array}{rcl} x^2-3x+2 &=& 0 \\\\ (x-1)(x-2) &=& 0 \\\\ x &=& 1, 2 \end{array}$$これが最も重要なポイントとなるのですが、例題1では $x$ が両端に、例題2では $x$ が中央に配置されるような回答の形となっています。
この形は不等号の向きによって決定され、与えられた2次不等式の関数側( $x$ を含む方)が0より大きい場合は $x$ が両端に、0より小さい場合は $x$ が中央に配置される形の回答となります。
問題文の不等号にイコールがついていれば、回答に含まれる不等号の全てにもイコールをつける(ついていなければつけない)という理解で十分です。
先述の3つのポイントを考慮して、グラフを描かずに2次不等式を解いてみましょう。
$x^2-2x-15 < 0$ を解け
マスマスターの思考回路

ポイント1にある、2次不等式を2次方程式としてみなしたときの解を求めるために、因数分解しましょう。
マスマスターの思考回路

2次不等式を2次方程式としてみなしたときの解は、$x=5, ~-3$ となります。
またポイント2について、関数側が0より小さいので $x$ が中央に配置されます。
さらにポイント3について、問題文の不等号にイコールがついていませんので、回答の不等号にもイコールをつける必要はありません。
以上により、
となります。
マスマスターの思考回路

$5 < x < -3$ と答えると不正解となります。
数値は小さい方を左、大きい方を右に書くということに注意しましょう。
次の例題では補足説明なしで回答しますが、ここまで理解できていれば問題ないでしょう。
$x^2+2x-8 \geqq 0$ を解け
よって、
となります。
$-x^2+7x-12 > 0$ を解け
マスマスターの思考回路

本例題では $x^2$ の係数が負の数となっているため、今までと異なり2次関数は上に凸となります。
その場合、ポイント2における式の形(回答の $x$ の配置)も逆転するのですが、それについて考える必要はありません。
与えられているのは2次関数でなく2次不等式ですから、 両辺に $-1$ をかけて $x^2$ の係数を正の数に変えてしまえば今までと同様に対応することができます。
( $-1$ をかけたときには、不等号の向きが逆転することに注意してください)
よって、
となります。
さて、ここまでが2次不等式の基本事項の説明となりますが、少し特殊な2次不等式というものも存在しますので、それらについて見ていきましょう。
$x^2-x-1 > 0$ を解け
マスマスターの思考回路

$x^2-x-1$ は簡単に因数分解できませんので、2次不等式を2次方程式に変えてしまい、解の公式を用いて2次方程式としての解を求める流れとなります。
$x^2-x-1 = 0$ の解は
$$\begin{array}{rcl} x &=& \cfrac{-(-1) \pm \sqrt{(-1)^2-4 \cdot 1 \cdot (-1)}}{2 \cdot 1} \\\\ x &=& \cfrac{1 \pm \sqrt{1 + 4}}{2} \\\\ x &=& \cfrac{1 \pm \sqrt{5}}{2} \\\\ \end{array}$$よって、
となります。
マスマスターの思考回路

$x = \cfrac{-(-1) \pm \sqrt{(-1)^2-4 \cdot 1 \cdot (-1)}}{2 \cdot 1} \\ > 0$ といったような不等号を含む途中式を書いてしまうと誤りとなります。
解の公式はあくまで2次「方程式」に対して成立するものであり「不等式」に対して成立するものではありません。
上述のように、与えられた2次不等式とは別に2次方程式を作成し、それに対して解の公式を適用するという流れで回答を作成しましょう。
$x^2-x+1 < 0$ を解け
マスマスターの思考回路

本例題も因数分解は難しそうですね?
例題6と同様に、解の公式を用いてみましょう。
$x^2-x+1 = 0$ の解は
$$\begin{array}{rcl} x &=& \cfrac{-(-1) \pm \sqrt{(-1)^2-4 \cdot 1 \cdot 1}}{2 \cdot 1} \\\\ x &=& \cfrac{1 \pm \sqrt{1 – 4}}{2} \\\\ x &=& \cfrac{1 \pm \sqrt{-3}}{2} \\\\ \end{array}$$マスマスターの思考回路

ルートの中身が $-3$ で負の数となっていますが、ルートの中身の数は負の数であってはなりません。
この場合は判別式の値が負、つまり実数解を持たないということですので、不等式の解として用いられる2数を求めることを諦めましょう。
そして、実数解がないのであれば、上の解の公式による計算は回答に用いる途中過程としては不要となりますので、次のように回答しましょう。
判別式
$$\begin{array}{rcl} D &=& (-1)^2-4 \cdot 1 \cdot 1 \\\\ &=& -3 < 0 \end{array}$$であることにより、すべての $x$ について、 $x^2-x+1 > 0$ が成立する。
よって、 $x^2-x+1 < 0$ の解は
解なし
となります。
マスマスターの思考回路

すべての $x$ について、 $x^2-x+1 > 0$ が成立するのは、 $y=x^2-x+1$ という2次関数が $x$ 軸と共有点を持たない、つまり、 $x$ 軸より上側にしか対象の2次関数のグラフが描画されないという理由からになります。
$x^2-x+1 > 0$ を解け
マスマスターの思考回路

本例題は例題7の不等号を逆向きにしたものとなっています。
例題7より、すべての $x$ について、 $x^2-x+1 > 0$ が成立するので、$x^2-x+1 > 0$ の解は
すべての実数
となります。
$-x^2+2x-1 \leqq 0$ を解け
マスマスターの思考回路

$x^2$ の係数が負の数となっていますが、どんな2次不等式が出題されても、先の例で見たように $x^2$ の係数を正に変えてしまいましょう。
マスマスターの思考回路

本例題では因数分解ができましたが、 かっこ2乗の形になっています。
つまり重解を持つので、回答に用いられる2つの数値は同じ値となります。
今までのように考えると、解は $x \leqq 1, 1 \leqq x$ となりますが、これはつまり $x$ が1以下または1以上ということですから、すべての実数を意味していることと同じになります。
$x \leqq 1, 1 \leqq x$ と回答した場合、間違いではありませんが、もっと簡潔な回答が可能であるという理由から原点の対象となるかもしれません。
よって、
すべての実数
となります。
マスマスターの思考回路

$(x-1)^2$ はそもそも平方数ですから、0以上の値以外の値をとることはありません。
この考え方に基づき、回答をすべての実数としても構いません。
$-x^2+2x-1 \geqq 0$ を解け
マスマスターの思考回路

本例題は例題9の不等号を逆向きにしたものです。
マスマスターの思考回路

今までのように考えると、解は $1 \leqq x \leqq 1$ となりますが、これはつまり $x$ が1以上かつ1以下ということですから、 $x=1$ を意味していることと同じになります。
$1 \leqq x \leqq 1$ と回答した場合、間違いではありませんが、もっと簡潔な回答が可能であるという理由から原点の対象となるかもしれません。
よって、
となります。
マスマスターの思考回路

不等式の解が、不等号でなくイコールで表される場合もあるということですね。
また、$(x-1)^2$ はそもそも平方数ですから、 $0$ または正の値しかとり得ません。
$(x-1)^2$ が $0$ 以下の値になるのはちょうど $0$ のときだけですので、 この考え方に基づき、回答を $x=1$ としても構いません。
$-x^2+2x-1 > 0$ を解け
マスマスターの思考回路

本例題は例題10の不等号のイコールを無くしたものです。
マスマスターの思考回路

今までのように考えると、解は $1 < x < 1$ となりますが、これはつまり $x$ が1より大きいかつ1より小さいということです。 それに該当する値は存在しませんので、解なしを意味していることと同じになります。 $1 < x < 1$ と回答した場合、間違いではありませんが、もっと簡潔な回答が可能であるという理由から原点の対象となるかもしれません。
よって、
解なし
となります。
マスマスターの思考回路

$(x-1)^2$ はそもそも平方数ですから、 負の数をとることはあり得ません。
この考え方に基づき、回答を解なしとしても構いません。
$-x^2+2x-1 < 0$ を解け
マスマスターの思考回路

本例題は例題11の不等号の向きを逆にしたものです。
マスマスターの思考回路

今までのように考えると、解は $x < 1, ~ 1 < x$ となりますが、これはつまり $x$ が1より小さいまたは1より大きいということであり、1以外の全ての実数を意味していることと同じになります。 $x < 1, ~ 1 < x$ と回答した場合、間違いではありませんが、もっと簡潔な回答が可能であるという理由から原点の対象となるかもしれません。
よって、
1以外の全ての実数
となります。
マスマスターの思考回路

$(x-1)^2$ はそもそも平方数ですから、 0以上の値以外をとることはあり得ず、ちょうど0となる場合を除けばいいということになります。
この考え方に基づき、回答を1以外の全ての実数としても構いません。
いかがでしたか?
不等式の解が、「解なし」や「全ての実数」といった式でないものになることもあり、慣れないうちはどういうときにどういう形の回答になるのかの判断をつけることは難しいかと思います。
しかし、迷った場合には2次関数のグラフを描き(慣れてきたら思い浮かべるだけも構いません)、不等式が意味するところが何なのかという観点で問題に向き合えば、自ずと答えが導かれることでしょう。
特に重要なことは、与えられた2次不等式の関数側( $x$ を含む方)が0より大きい場合は $x$ が両端に、0より小さい場合は $x$ が中央に配置される形の回答となることであり、このパターンに該当する問題が多数を占めますので、しっかり覚えておくようにしましょう。
【基礎】二次関数のまとめ
この記事が気に入ったら
「いいね」しよう!
-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。
>> お問い合わせ
>> プライバシーポリシー
2次関数のグラフと2次方程式の関係で見たように、不等式についても2次関数のグラフと関連付けをし幾何的に解きましょう。
まずはグラフを書いてみます。