基礎知識

ここでは、2次関数のグラフと2次方程式の関係性についての説明を行います。

2次方程式それ自体は代数的なものですが、2次関数のグラフと関連付けることにより、幾何的な視点で見ることができるようになることでしょう。

2次関数とは？2次方程式とは？

2次関数は次のように表される関数です。

2次方程式は次のように表される方程式です。

マスマスターの思考回路

つまり、2次関数の を にしたものが2次方程式だということですね。

そして、このことが重要な意味を持つこととなります。

2次方程式は、2次関数とx軸の交点にある

ここで、下図のような適当な2次関数のグラフを考えましょう。

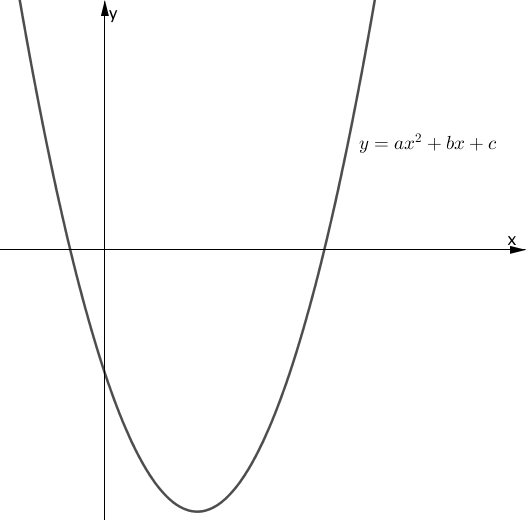
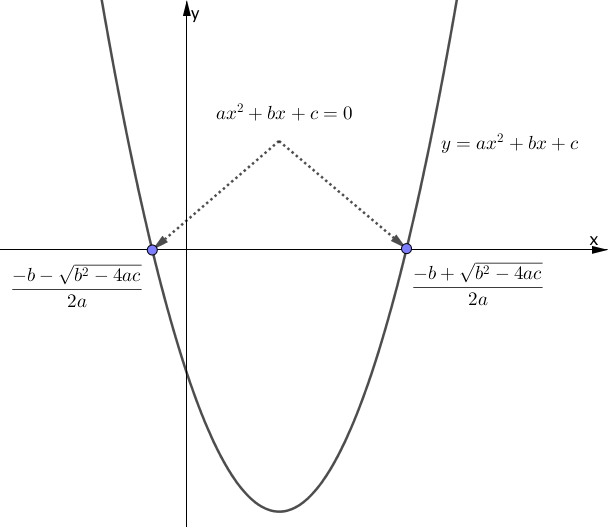
先述のように、2次関数の を にしたものが2次方程式ですので、上図の2次関数の が になる箇所、つまり2次関数と 軸の交点が2次方程式を意味しているということになります。

マスマスターの思考回路

2次関数と 軸の交点が2次方程式であり、2次方程式の解がそれらの 座標となります。

2次方程式の解の判別式と2次関数のグラフ

さて、2次関数と 軸との交点の 座標は2次方程式の解となるのですが、必ずしも2次関数が 軸との交点を持つとは限りません。

2次方程式の解があるかないかは判別式により判断可能ですので、判別式と2次関数のグラフとの関係性を次に見ていきましょう。

判別式 D > 0 のとき

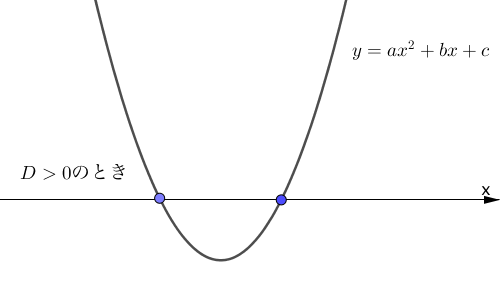
のとき、2次方程式は異なる二つの実数解を持ちます。

つまり、2次関数が 軸と異なる2点で交わるということを意味しており、グラフは下のようになります。

マスマスターの思考回路

軸は判別式とは無関係であり、 軸と2次関数のグラフとの関係性が重要なため、上図から除いています。

判別式 D = 0 のとき

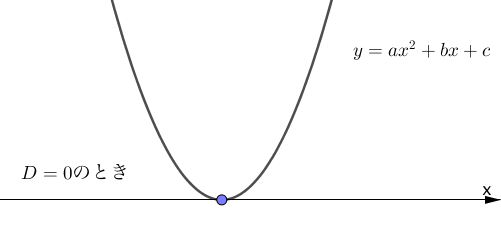
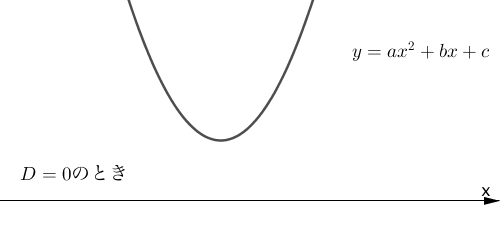
のとき、2次方程式は重解を持ちます。

つまり、2次関数が 軸と1点で接するということを意味しており、グラフは下のようになります。

判別式 D < 0 のとき

のとき、2次方程式は実数解を持ちません。

つまり、2次関数が 軸との共有点を持たないということを意味しており、グラフは下のようになります。

マスマスターの思考回路

判別式により2次方程式の解の個数がわかるので、2次関数と 軸との共有点の個数もわかるということになります。

2次関数のグラフと2次方程式の説明のおわりに

いかがでしたか？

本記事の内容自体が直接的に問題として出題されることはあまり無いかと思われますが、二次不等式を解くためにとても重要な内容となります。

代数的な問題を幾何と関連づけることは今後もよくありますので、この段階でしっかり理解しておくと良いでしょう。