【基礎知識】乃木坂46の「いつかできるから今日できる」を数学的命題として解釈する
- 命題
基礎知識
基礎知識
中学校で学習した二次関数(放物線)の式は $y=ax^2$ という形をしていましたが、高校で学習する二次関数は $y=a(x-p)^2 +q$ という形になります。
このような式で表すことにより、頂点が原点に一致しないような放物線を表現することができます。
具体例を通して理解していきましょう。
例として $y=x^2+1$ という関数について考えましょう。
各種 $x$ の値に対応する $y$ の値を計算すると下の表のようになります。
$$ \begin{array}{c||c|c|c|c|c} x & -2 & -1 & 0 & 1 & 2 \\ \hline y & 5 & 2 & 0 & 2 & 5 \\ \end{array} $$マスマスターの思考回路

上の表の値を用いてグラフを書くと、 $y=x^2+1$ は下の図の赤線のようになります。
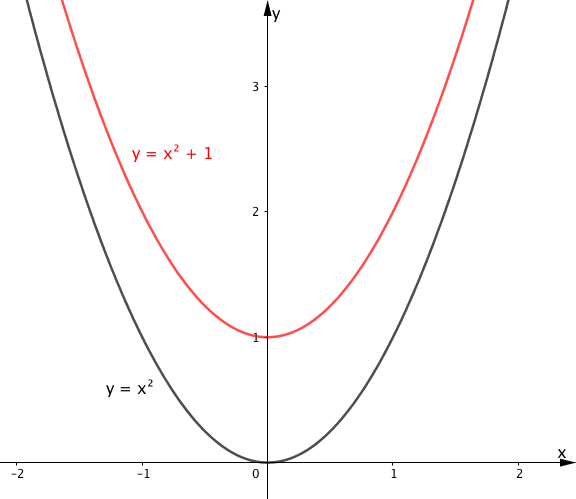
上図から、$y=x^2+1$ のグラフは $y=x^2$ のグラフを $y$ 軸の正の方向に $1$ だけ移動させたものであることがわかります。
マスマスターの思考回路

一般に、 $y=x^2+q$ のグラフは $y=x^2$ のグラフを $y$ 軸の正の方向に $q$ だけ移動させたものになります。
例として $y=(x-1)^2$ という関数について考えましょう。
各種 $x$ の値に対応する $y$ の値を計算すると下の表のようになります。
$$ \begin{array}{rcl} \begin{array}{c||c|c|c|c|c|c} \hline x & -2 & -1 & 0 & 1 & 2 & 3 \\ \hline y & 9 & 4 & 1 & 0 & 1 & 4 \\ \hline \end{array} \end{array} $$上の表の値を用いてグラフを書くと、 $y=(x-1)^2$ は下の図の赤線のようになります。
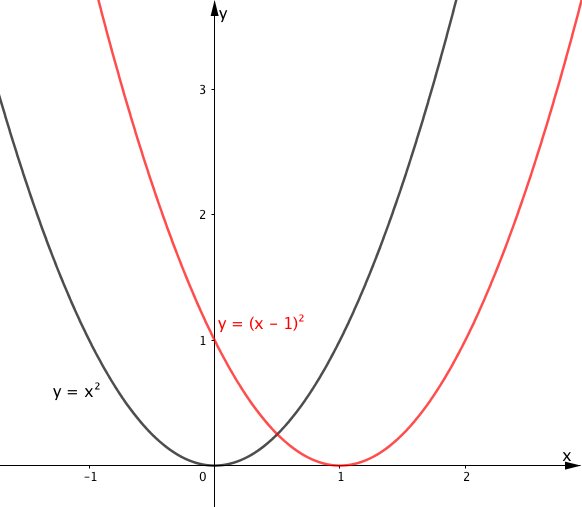
上図から、$y=(x-1)^2$ のグラフは $y=x^2$ のグラフを $x$ 軸の正の方向に $1$ だけ移動させたものであることがわかります。
マスマスターの思考回路

一般に、 $y=(x-p)^2$ のグラフは $y=x^2$ のグラフを $x$ 軸の正の方向に $p$ だけ移動させたものになります。
例として $y=(x-1)^2+1$ という関数について考えましょう。
各種 $x$ の値に対応する $y$ の値を計算すると下の表のようになります。
$$ \begin{array}{rcl} \begin{array}{c||c|c|c|c|c|c} \hline x & -2 & -1 & 0 & 1 & 2 & 3 \\ \hline y & 10 & 5 & 2 & 1 & 2 & 5 \\ \hline \end{array} \end{array} $$上の表の値を用いてグラフを書くと、 $y=(x-1)^2+1$ は下の図の赤線のようになります。
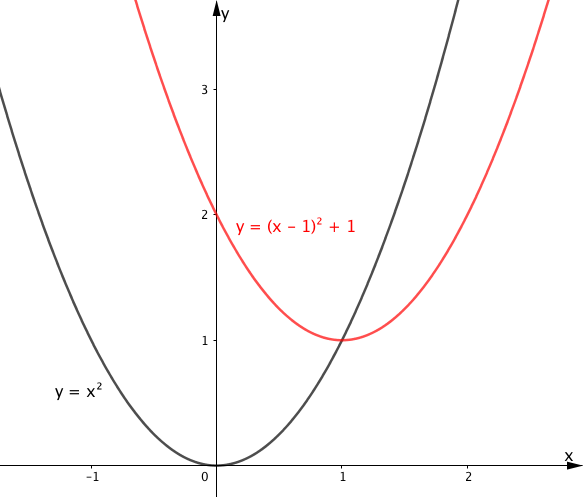
ここまでの例で見てきたように、 $y=x^2+1$ は右辺の末尾にある $+1$ により $y$ 軸の正の方向に $1$ だけ移動されました。
また、$y=(x-1)^2$ は右辺の $x$ が $x-1$ となることにより $x$ 軸の正の方向に $1$ だけ移動されました。
この $y=(x-1)^2$ に対し、右辺の末尾に $+1$ をつけた関数である$y=(x-1)^2+1$ は、$x$ 軸の正の方向に $1$ だけ移動されつつ、 $y$ 軸の正の方向にも $1$ だけ移動されると考えると上のようなグラフになることが理解できるかと思います。
マスマスターの思考回路

一般に、 $y=(x-p)^2+q$ のグラフは $y=x^2$ のグラフを $x$ 軸の正の方向に $p$ 、$y$ 軸の正の方向に $q$ だけ移動させたものになります。
前の例で見たように $y=(x-p)^2+q$ という形の式で表現された二次関数は、頂点の座標を原点以外の場所であっても自由にとることが可能であることがわかりました。
しかし、冒頭で述べた高校で学習する二次関数の形は $y=a(x-p)^2 +q$ であり、$y=(x-p)^2+q$ は $a=1$ のときの特殊な場合にすぎません。
$y=a(x-p)^2 +q$ のグラフはどのような概形となるのでしょうか?
答えは簡単で、 $y=a(x-p)^2 +q$ の $a$ は、中学で学習した $y=ax^2$ の $a$ の役割と同じです。
$a$ が正のときは下に凸、負のときは上に凸、 $a$ の絶対値が大きいほどグラフの開き方が狭くなる、といったものでしたね?
例として、$y=2(x-1)^2$ のグラフを見てみましょう
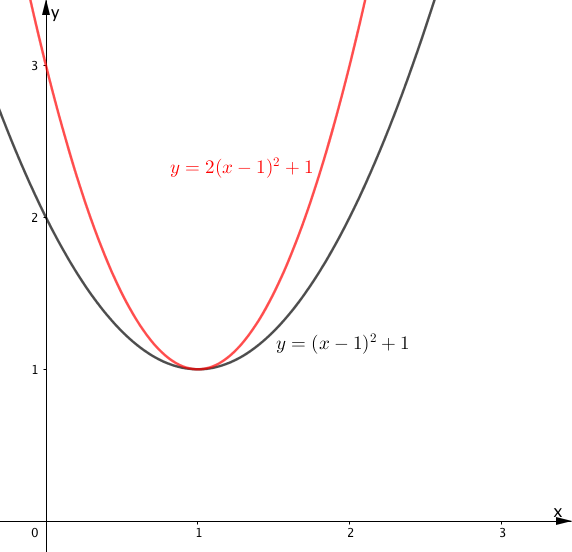
$y=2(x-1)^2$ は $y=(x-1)^2$ のグラフの開き方より狭く、関係性としてはそれぞれ $y=2x^2$ と $y=x^2$ のグラフと同じと理解すると良いでしょう。
いかがでしたか?
$y=a(x-p)^2 +q$ という形で二次関数を表現することにより、頂点の位置が原点以外の位置をとりうるという点が、中学で学習した内容との違いになります。
$y=a(x-p)^2 +q$ は 軸 $x=p$ 、頂点 $(p, q)$ の放物線であるといい、 式を形作る $p, q$ は頂点の座標そのものを意味しています。
また放物線は $y=ax^2+bx+c$ という形で表現されることもありますが、この形で表されると頂点の座標を知ることができません。
マスマスターの思考回路

頂点の座標がわからない場合、グラフがどのような形でどこに位置するかがわからず不都合となる場合が多くあります。
その場合は平方完成という手段により$y=a(x-p)^2 +q$ に変形することで頂点の座標を求める事となります。
平方完成の方法については下の記事を参考にしてください。
【二次関数】平方完成の方法
また本記事の内容は平行移動を学習する事で、より理解が深まるかと思います。
平行移動については下の記事を参考にしてください。
【公式】関数の平行移動について
二次関数の問題では「グラフをかく」ということが基本となりますので、しっかり理解しておきましょう。
【基礎】二次関数のまとめ
この記事が気に入ったら
「いいね」しよう!
-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。
>> お問い合わせ
>> プライバシーポリシー
グラフの概形を知らなくても、関数がとりうる $x$ と $y$ の値の組を座標平面上に点として打っていき、それらを滑らかに結ぶことでグラフを書くことは可能です。