基礎知識

平方完成は二次方程式の解の公式の導出や、二次関数の頂点を求める際に必要となる式変形の方法です。

平方完成は通常の四則演算のような手順とは全く異なる手順で進んでいくので、初めて平方完成を学んだ時にはあっけにとられてしまうかもしれません。

ここでは、平方完成の方法を順を追って説明していきます。

平方完成とは

平方完成とは、

$$\begin{array}{rcl} ax^2+bx+c \end{array}$$

という式を

$$\begin{array}{rcl} ax^2+bx+c &=& a(x-p)^2+q \end{array}$$

の形に変形することをいいます。

平方完成の手順

$2x^2-12x+22$という式を例として、平方完成の手順について説明していきます。

手順1

まず、$x^2$の係数で$x^2$と$x$を含む項をくくります。

$$\begin{array}{rcl} 2x^2-12x+22　&=& 2(x^2-6x) + 22 \end{array}$$

手順2

この手順が重要になります。次のようにしてください。

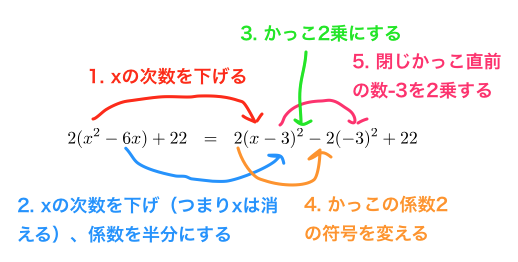
上の式変形は一つの手順内に5つもやらなければならないことがありますが、この5つを同時に行って初めて一つの式が完成します。
なぜこのようにすればよいかは後述します。

手順3

最後に、下の式の赤線部だけを計算します。

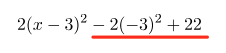
$2(x-3)^2 -2(-3)^2 + 22 \\$
$= 2(x-3)^2 -2(9) + 22 \\$
$= 2(x-3)^2 -18 + 22 \\$
$= 2(x-3)^2 + 4$

平方完成結果

$2(x-3)^2 + 4$は式の形としては$a(x-p)^2+q$の形になっているので、これで平方完成ができたことになります。

よって、$2x^2-12x+22$を平方完成すると、

$$\begin{array}{rcl} 2x^2-12x+22 = 2(x-3)^2 + 4 \end{array}$$

となります。

手順2の詳しい解説

上の手順に従えば平方完成はできるのですが、手順2のような式変形がなぜ成り立つのかについて、途中式を交えて詳しく見ていきたいと思います。

まず、平方完成というのはかっこの２乗の形にすることが目的ですから、$x^2-6x$を無理やりその形に変形するということになります。

そのために、下の展開の公式を利用します。

$$\begin{array}{rcl} (x-a)^2 = x^2 -2ax + a^2 \end{array}$$

上の式を変形すると、

$$\begin{array}{rcl} x^2 -2ax = (x-a)^2 – a^2 \end{array}$$

となります。これを用いると、

$2(x^2-6x) + 22 = 2\{ (x – 3)^2 – (-3)^2 \} + 22$

と変形する事ができ、中括弧の前にある2を$(x – 3)^2$と$- (-3)^2$に分配すると、

$2\{ (x – 3)^2 – (-3)^2 \} + 22 = 2(x – 3)^2 – 2(-3)^2 + 22$

と変形する事ができます。

以上により、

$2(x^2-6x) + 22 = 2(x – 3)^2 – 2(-3)^2 + 22$

となるので、下のような手順2の変形を行えば、途中計算を省いて即座にかっこの２乗の形に変形できるということになります。

平方完成の説明のおわりに

いかがでしたか？

平方完成を行うにはとにかく慣れが必要です。
係数に文字が含まれていたとしても、素早く正確に平方完成を行える事が要求されますので、十分に練習を重ねてください。

【基礎】二次関数のまとめ