学校や塾では教えてくれない、元塾講師の思考回路の公開

公式

【確率】条件付き確率の公式とその例題

確率の問題では、ある事象Aが起こったことがわかっている場合に、ある事象Bも起こっている確率を求めるような場合があり、これを条件付き確率といいます。

ここでは条件付き確率の公式と、その具体例の解説を行っていきます。

条件付き確率の公式

Aが起こる確率をP(A)、AとBが同時に起こる確率をP(A \cap B)とし、
事象Aが起こったことがわかっている場合に、ある事象Bも起こっている確率をP_A(B)と表すとき、条件付き確率P_A(B)は、

    \begin{eqnarray*} P_A(B) &=& \cfrac{P(A \cap B)}{P(A)} \\\\ \end{eqnarray*}

条件付き確率の公式の説明

条件付き確率については、ベン図を用いると直感的に理解できるかと思います。

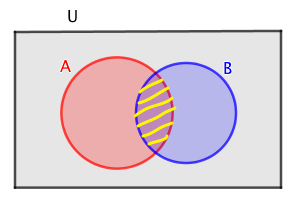
条件付き確率の公式

条件付き確率の式、

    \begin{eqnarray*} P_A(B) &=& \cfrac{P(A \cap B)}{P(A)} \\\\ \end{eqnarray*}

は、その式の形から、P(A)に対するP(A \cap B)の比を意味しており、それは上図における赤色部分に対する黄色部分の比になります。
そしてこれは、全事象をAとみなしたときのBの起きる確率であるということができます。

つまり条件付き確率とは、何を全事象とみなすかというところが要点になるわけです。

ここで、Aの起きる確率P(A)（条件付き確率でない）を、全事象をUとみなしたときのAの起きる条件付き確率として求めると、

    \begin{eqnarray*} P_U(A) &=& \cfrac{P(U \cap A)}{P(U)} \\\\ &=& \cfrac{P(A)}{1} \\\\ &=& P(A) \\\\ \end{eqnarray*}

と考えることができ、ちゃんとP(A)という結果になりますね？
だから条件付き確率でない普通の確率も、条件付き確率の一種であるということがわかります。

条件付き確率の例題

ここで、条件付き確率の例題を解いてみましょう。

例題：　さいころを1回ふり、出た目が偶数であることがわかっている場合に、その目が2である確率を求めよ。

条件付き確率の公式を使う場合

下の公式を使って確率を求めましょう。

Aが起こる確率をP(A)、AとBが同時に起こる確率をP(A \cap B)とし、
事象Aが起こったことがわかっている場合に、ある事象Bも起こっている確率をP_A(B)と表すとき、条件付き確率P_A(B)は、

    \begin{eqnarray*} P_A(B) &=& \cfrac{P(A \cap B)}{P(A)} \\\\ \end{eqnarray*}

偶数の目が出る確率をP(A)、２の目が出る確率をP(B)とします。

偶数の目が出る確率は、

    \begin{eqnarray*} P(A) &=& \cfrac{3}{6} \\\\ \end{eqnarray*}

となります。

偶数の目が出てかつ2の目が出る（つまり2の目が出る）確率は、

    \begin{eqnarray*} P(A\cap B) &=& \cfrac{1}{6} \\\\ \end{eqnarray*}

となります。

よって、

求める条件付き確率P_A(B)は、

    \begin{eqnarray*} P_A(B) &=& \cfrac{P(A \cap B)}{P(A)} \\\\ &=& \cfrac{ \cfrac{1}{6} }{ \cfrac{3}{6} } \\\\ &=& \cfrac{1}{3} \\\\ \end{eqnarray*}

となります。

条件付き確率の公式を使わない場合

マスマスターの思考回路

全事象を、偶数の目が出ることとみなして条件付き確率を考えましょう。

偶数の目の出方は2, 4, 6 の3通り、
2の目が出るのは1通り、

よって求める条件付き確率は

    \begin{eqnarray*} \cfrac{1}{3} \end{eqnarray*}

となります。

条件付き確率の説明の終わりに

いかがでしたか？

条件付き確率の公式は少し覚えにくいところがありますが、ベン図による理解をしておけば、公式を覚えていなくても条件付き確率を求めることができます。

また条件付き確率でない通常の確率も、条件付き確率の一種にすぎない（つまり条件付き確率というものは、特別なものではない）ことを知っておくと良いかと思います。

【確率】場合の数と確率のまとめ

公式

確率

プロフィール

-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。

検索

この記事の目次

関連記事

サイドメニュー