学校や塾では教えてくれない、元塾講師の思考回路の公開

基礎知識

【基礎知識】ベクトルの演算

前回の記事【基礎知識】ベクトルとその意味について で、ベクトルとは何かについてお話ししました。

今回の記事ではベクトルの和・差といったベクトルの演算方法についての説明を行っていきます。

逆ベクトル

\overrightarrow{AB} と大きさが等しく、向きが反対であるベクトルを -\overrightarrow{AB} と表し、これを\overrightarrow{AB} の逆ベクトルといいます。

下のような図を考えましょう。

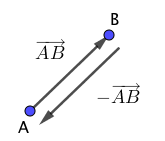
逆ベクトル

上図より、 -\overrightarrow{AB} は \overrightarrow{BA} と表すこともできますので、

    \begin{eqnarray*} -\overrightarrow{AB} &=& \overrightarrow{BA} \\\\ \end{eqnarray*}

が成り立ちます。

マスマスターの思考回路

つまり、ベクトルの始点と終点を入れ替え、-1倍すると自分自身と同じベクトルを意味するということになります。

零ベクトル

大きさが0のベクトルを零（ゼロ）ベクトルといい、 \overrightarrow{0} と表します。

ベクトルの大きさはそのベクトルの始点から終点までの最短距離のことですので、例えば始点と終点が共に点 A のベクトル \overrightarrow{AA} を考えた場合にこれは零ベクトルとなり、

    \begin{eqnarray*} \overrightarrow{AA} = \overrightarrow{0} \\\\ \end{eqnarray*}

が成り立ちます。

ベクトルの和

複数のベクトルを足し合わせた結果を、一つのベクトルとして表現することができます。

下図の\overrightarrow{AB}と\overrightarrow{DE}の和を考えます。

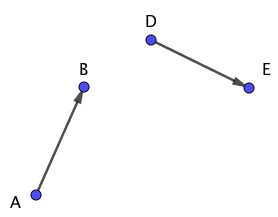
ベクトルの和

ベクトルの和を考えるときにはまず、一方のベクトルの始点を他方のベクトルの終点に重ね合わせます。
ベクトルはその存在位置は対象としないので、平行移動によってベクトルを移動させても問題ありません。
下図のように点Dが点Bに重なるようにベクトル\overrightarrow{DE}を平行移動させます。

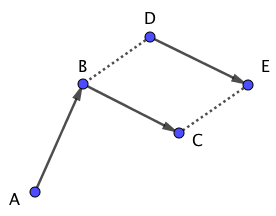
ベクトルの和

点Aと点Cを結び、\overrightarrow{AC}を定義します。

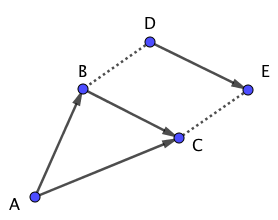
ベクトルの和

上図について、

    \begin{eqnarray*} \overrightarrow{AB} + \overrightarrow{BC}　&=& \overrightarrow{AC}\\\\ \end{eqnarray*}

が成り立ち、これをベクトルの和といいます。

上の式は、点Aから点Bを経由して点Cへ移動することは、点Aから点Cへまっすぐ移動したとみなすということを意味しています。
つまり、ベクトルの和はその経由地点は無関係であり、スタート地点とゴール地点で決まるということです。

マスマスターの思考回路

\overrightarrow{AB} + \overrightarrow{BC} は終点の B と始点の B がくっついて無くなり、 \overrightarrow{AC} というベクトルになると考えると理解しやすいかと思います。

ベクトルの和を考えるには、一方のベクトルの始点が他方のベクトルの終点に一致していることが前提となります。
しかしあるベクトルを平行移動させたとき、平行移動前後のベクトルは相等ですから、どんなベクトルでも始点と終点を一致させることができます。

これにより、

    \begin{eqnarray*}\overrightarrow{AB} + \overrightarrow{DE}　&=& \overrightarrow{AB} + \overrightarrow{BC}\\\\&=& \overrightarrow{AC}\\\\\end{eqnarray*}


のようにベクトルの和を求めることができます。

ベクトルの差

次の式のようなベクトルの差の式が成立します。

    \begin{eqnarray*} \overrightarrow{AB} &=& \overrightarrow{OB} -\overrightarrow{OA} \\\\ \end{eqnarray*}

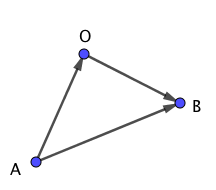
ベクトルの差

上図についてベクトルの和を用いると、

    \begin{eqnarray*} \overrightarrow{AB} &=& \overrightarrow{AO} + \overrightarrow{OB} \\\\ \end{eqnarray*}

と表すことができます。上式を \overrightarrow{AO} の逆ベクトル \overrightarrow{OA} を用いて表すと、

    \begin{eqnarray*} \overrightarrow{AB} &=& -\overrightarrow{OA} + \overrightarrow{OB} \\\\ &=& \overrightarrow{OB} -\overrightarrow{OA} \\\\ \end{eqnarray*}

よって、

    \begin{eqnarray*} \overrightarrow{AB} &=& \overrightarrow{OB} -\overrightarrow{OA} \\\\ \end{eqnarray*}

が成り立ちます。

マスマスターの思考回路

\overrightarrow{AB} はA と B を入れ替えつつ、適当な点 O を仲介して \overrightarrow{OB} -\overrightarrow{OA} と表されるということになります。

ベクトルの実数倍

下の正六角形について考えます。

正六角形

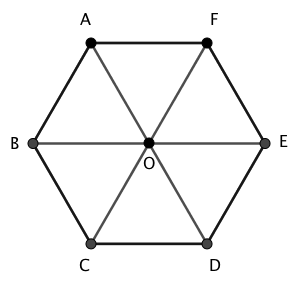
ベクトルの和から、

    \begin{eqnarray*}\overrightarrow{DA} &=& \overrightarrow{DO} + \overrightarrow{OA} \\\\\end{eqnarray*}


が成り立ちます。

線分DOと線分OAの長さは等しく、その方向も同じなので、\overrightarrow{DO} = \overrightarrow{OA}が成り立ちます。
このとき、

    \begin{eqnarray*}\overrightarrow{DA} &=& \overrightarrow{DO} + \overrightarrow{OA} \\\\&=& \overrightarrow{OA} + \overrightarrow{OA} \\\\&=& 2\overrightarrow{OA}\\\\\end{eqnarray*}

となります。

2\overrightarrow{OA}の2の部分は\overrightarrow{OA}というベクトルを2倍していることになりますが、ベクトルの2倍（実数倍）とは何なのでしょうか？
ベクトルは「大きさ」と「方向」を持ちますので、「大きさ」も「方向」も２倍になるのでしょうか？

その答えは上図から得られます。
図の\overrightarrow{OA}を、方向は変えずに2倍の大きさにする（つまり、点Oを点Dに重なるように動かす）と、\overrightarrow{DA}に一致することがわかるかと思います。

つまりベクトルの実数倍はそのベクトルの大きさのみを対象としており、実数倍することによってベクトルの方向は変わらないということになります。

ベクトルの負の数の実数倍

先ほどの例ではベクトルの2倍（+2倍）を考えましたが、ベクトルに負の数をかけた場合はどうなるのでしょうか？
これについては、初めて正負の数を学んだときの考え方と同様に考えることができます。

下図の数直線を考えます。

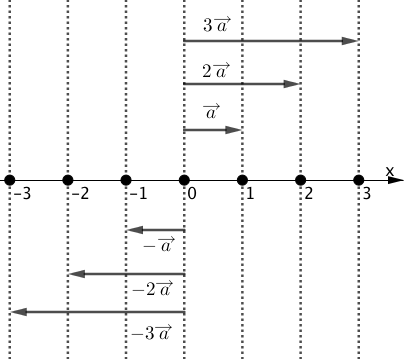
ベクトルの負の数の定数倍

x軸に平行で大きさが1のベクトルを\overrightarrow{a}とします。
\overrightarrow{a}を実数倍した各種ベクトルk\overrightarrow{a}は、
k>0ならば、\overrightarrow{a}と同じ向きに、
k<0ならば、\overrightarrow{a}と逆の向きに、
\overrightarrow{a}の大きさを|k|倍したベクトルであると言えます。

マスマスターの思考回路

つまり平たくいうと、ベクトルに負の数をかけると向きが逆になるということです。

ベクトルの平行

ベクトルを実数倍すると方向はそのままで、大きさのみを自由に変えることができます。（負の数をかけると真逆の向きになりますが、始点と終点の区別を無視すれば方向としては同じと考えます）

これを利用して、次のようなベクトルの平行条件が導かれます。

ベクトルの平行条件

\overrightarrow{a}　\neq　\overrightarrow{0}, \overrightarrow{b}　\neq　\overrightarrow{0}である二つのベクトルに対し、\overrightarrow{b}　=k\overrightarrow{a}となる実数kが存在すること。

\overrightarrow{a}　\neq　\overrightarrow{0}, \overrightarrow{b}　\neq　\overrightarrow{0}が、ベクトルの平行条件を論じる上での前提となっています。
これは、対象とするベクトルが零ベクトルであればそのベクトルは点になってしまうので、平行かどうかを論じることができないためです。

\overrightarrow{b}　=k\overrightarrow{a}については、\overrightarrow{a}の大きさをk倍すれば、\overrightarrow{b}に一致するということを意味しています。
\overrightarrow{a} というベクトルを k 倍した結果として二つのベクトルが一致する（ような実数kが存在している）のであれば、そもそもその二つのベクトルは平行でなければならない、という事がこの式の意味するところになります。

マスマスターの思考回路

k\overrightarrow{a} とはつまり、方向は変えずに大きさだけを k 倍するという意味になります。
ここで、k < 0 のときは向きは逆になるのですが、向きが逆になっても直線としての方向は変わりませんので、ベクトルが平行であるかどうかに影響しません。

「大きさ」と「方向」が等しいベクトルは同じベクトルであるとみなすのですが、ベクトルの実数倍（大きさの操作）を行うだけでベクトルの相当が実現できるならば、そもそもその二つは平行であるということですね。

ベクトルの演算の説明の終わりに

いかがでしたか？

ベクトルは「大きさ」と「方向」を持つ量なので、「方向」についてそれらを足したり引いたりといったことはイメージしにくい内容だったかと思います。

今後、ベクトルは和で考えるよりも差で考える機会の方が多くなりますので、特にベクトルの差については十分な理解をしておきましょう。

【基礎知識】平面上のベクトルのまとめ

基礎知識

ベクトル

プロフィール

-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。

検索

この記事の目次

関連記事

サイドメニュー