基礎知識

「大きさ」と「方向」をもった量をベクトルといいます。
ベクトルを習うまでの数値計算は「大きさ」のみを対象としていましたが、ベクトルでは「大きさ」のみならず「方向」も考慮することになります。
計算内容自体はそれほど複雑なものにはなりにくいのですが、基礎知識の習得には苦労を要するかもしれません。

ベクトルは物理への応用性も高いので、しっかり理解しておきましょう。

ベクトルとその意味

線分 に から へ向きをつけて考えるとき、これを有向線分 といい、 を始点 を終点といいます。

マスマスターの思考回路

有向線分とはその名の通り、「向」きが「有」る「線分」であるという意味になります。

から へ向きをつけて考えた場合は有向線分 となりますが、これは有向線分 と異なるものとして扱います。

また、有向線分はその線分が存在する「位置」「向き」「大きさ」で定まるものとし、有向線分の「位置」を問題とせず、「向き」「大きさ」で定まる量をベクトルといいます。

ベクトルの相等

「相等」とは「同じ」であるということです。

下図の平行四辺形ABCDに対し、二つのベクトルとを考えます。

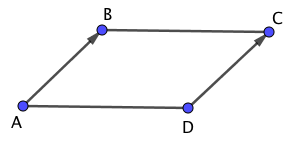
ベクトルは「大きさ」と「方向」を扱うものですので、「大きさ」と「方向」が同じであれば、同じベクトルであると考えます。
つまり、とは同じベクトルであるとみなし、このとき、

と表します。

つまり、ベクトルが存在している「位置」は違っても、「大きさ」と「方向」が同じであれば同じベクトルとみなすということです。

言い換えれば、あるベクトルが平行移動により、向きも含めて他方のベクトルにちょうど重なるとき、その二つのベクトルは等しいということもできます。

単位ベクトル

ベクトル の長さ（始点 から終点 までの最短距離）をベクトル の大きさといいます。

特に、大きさが1であるベクトルを単位ベクトルといいます。

ベクトルとその意味の説明の終わりに

有向線分という言葉自体は高校数学のベクトルを学習する上でほぼ使うことはありませんので、覚えておかなくてよいかと思います。

ベクトルは位置が不問であるということは重要ですので、このことはしっかり覚えておきましょう。