【基礎知識】乃木坂46の「いつかできるから今日できる」を数学的命題として解釈する
- 命題
基礎知識
基礎知識
【確率】余事象を用いた確率の求め方
ある確率を求める際には、そのことが起きる全ての場合を考えるということが基本となります。
「全ての場合」を対象としますので、その全ての場合というものが現実的に数えられる程度の物量でなくては、全てを数えあげることはできないと言えるでしょう。
しかし、その「全ての場合」が多ければ多いほど、余事象を用いることによって楽に確率を求めることができます。
ここでは余事象の基本的な考え方と、実例を紹介していきます。
余事象とは
ある事象$A$に対し$A$が起こらないという事象を$A$の余事象といいます。
余事象の確率は次の式によって求めることができます。
事象$A$が起こる確率を$P(A)$、事象$A$の余事象が起こる確率を$P(\overline{A})$と表すとき、その余事象の確率は、
$$\begin{array}{rcl} P(\overline{A}) &=& 1 – P(A) \end{array}$$余事象の確率の説明
全事象を$U$とすると、確率の最大値は$1$なので$P(U)=1$となります。
全事象に含まれる部分的な事象を$A$とするとき、全事象内のそれ以外の事象が余事象$\overline{A}$となります。
これを図にすると下のようになります。
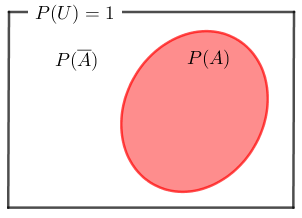
上図について、赤色の部分が事象Aが発生する確率$P(A)$を意味しており、黒枠内の赤色でない部分が余事象の確率$P(\overline{A})$を意味します。
この二つの部分を合わせるとちょうど黒枠部になることから、
となり、上式を$\overline{A}$について解くと、
$$\begin{array}{rcl}
P(\overline{A}) = 1 -P(A)
\end{array}$$
が成り立ちます。
余事象の確率の例題
次の例題を考えましょう。
コインを10回投げたとき、表が1回以上出る確率を求めよ
マスマスターの思考回路
余事象を利用せずに、互いに排反な反復試行の確率と捉えて確率を求めようとすると、
${}_{10} \mathrm{C}_ {1} \left(\cfrac{1}{2}\right)^{1} \left(\cfrac{1}{2}\right)^{9} + {}_{10} \mathrm{C} _{2} \left(\cfrac{1}{2}\right)^{2} \left(\cfrac{1}{2}\right)^{8} + \cdots + {}_{10} \mathrm{C} _{10} \left(\cfrac{1}{2}\right)^{10} \left(\cfrac{1}{2}\right)^{0}$
となります。
マスマスターの思考回路
とてもではないですが上式を計算する気にはなりませんね。
ここで余事象を考えてみましょう。
表が1回以上出ることの余事象は、表が1回も出ない、つまり裏が10回連続で出るということになります。
余事象を利用して確率を求めると、
$$\begin{array}{rcl} 1 – \left(\cfrac{1}{2}\right)^{10} \end{array}$$となります。
マスマスターの思考回路
この問題の場合では、余事象を利用しない場合は10個の確率の足し算を行わなければなりませんが、余事象を利用すると1個の確率を全事象の確率（=1）から引けば簡単に求められることとなります。
余事象を用いた確率を計算していくと、
$$\begin{array}{rcl} \cfrac{2^{10} – 1}{2^{10}} &=& \cfrac{1024 – 1}{1024} \\\\ &=& \cfrac{1023}{1024} \\\\ \end{array}$$となります。
余事象の説明の終わりに
いかかでしたか？
ある確率は、それが起こらない確率を求めることによって求めることができる、という事が余事象を用いた確率の意味するところになります。
直接的に確率を求める方法と、余事象を利用して確率を求める方法のどちらが楽かを判断したうえで、確率の問題に取り組みましょう。
【確率】場合の数と確率のまとめ
この記事が気に入ったら
「いいね」しよう！
プロフィール
-このサイトの記事を書いている人-
某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。
お問い合わせ
>> お問い合わせ
>> プライバシーポリシー
表が1回以上出るということは、表が1回、2回、 $\cdots$ 、10回出る確率の和になります。
つまり、これら10個の確率を求め、それらを足し算すると求めることができます。