【基礎知識】乃木坂46の「いつかできるから今日できる」を数学的命題として解釈する
- 命題
基礎知識
基礎知識
【基礎】指数関数とそのグラフ
ここでは指数関数とは何か、またそのグラフはどのような概形となるかについてお話ししていきたいと思います。
指数法則についての理解が必要となりますので、不安な方は指数法則を復習しておきましょう。
【指数関数】指数法則について説明するよ
目次
指数関数とは
$a$ を1でない正の定数とするとき
$$\begin{array}{rcl}
y = a^x
\end{array}$$
の形で定義される関数を $x$ の指数関数といい、 $a$ をその底（てい）といいます。
指数関数の底の値の条件
底 $a$ にはとりうる値の範囲に、次のような条件が設けられています。
$$\begin{array}{rcl}
a > 0, ~a \neq 1
\end{array}$$
底は正の数でなければならない
仮に $a < 0$ の場合を考えてみましょう。
例 : $a=-2, x = \cfrac{1}{2}$ のとき、
$$\begin{array}{rcl} y &=& (-2)^\frac{1}{2} \\\\ &=& \sqrt{-2} \\\\ &=& \sqrt{2}i \\\\ \end{array}$$このように $y$ の値が複素数となることがあります。
マスマスターの思考回路
底は1であってはならない
底が1の場合の $y=a^x$ は、
$$\begin{array}{rcl} y &=& a^x \\\\ &=& 1^x \\\\ &=& 1 \\\\ \end{array}$$となります。
底が1のときは1を何乗したとしても1にしかならないので、指数関数ではなく定数関数となります。
マスマスターの思考回路
実際には指数関数が定数関数となってしまうこと自体に、数学的な問題はありません。
底が1であってはならない理由はおそらく、問題を解く際に指数関数が定数関数となる場合をいちいち考える手間を省けるようにするためではないかと思われます。
また、 $a>0$ の条件からわかるように、 $a=0$ の場合が除外されていることも、底が1であってはならないことの理由と同様に、定数関数となる場合を除外するためのものでしょう。
ともかく底が0, 1となる場合が除外されていることで回答者の手間が省けることは事実ですので、ルールとして覚えてしまいましょう。
指数関数のグラフ
指数関数のグラフは非常に単純ですが、底の値によって概形が異なることに注意しましょう。
底の値によらず、次の三つの項目については共通する性質となります。
- y切片の値は1
- 定義域は実数全体
- 値域は正の数全体
それでは実際にグラフを見てみましょう。
1 < a のとき
0 < a < 1 のとき
底の値によるグラフの概形の違い
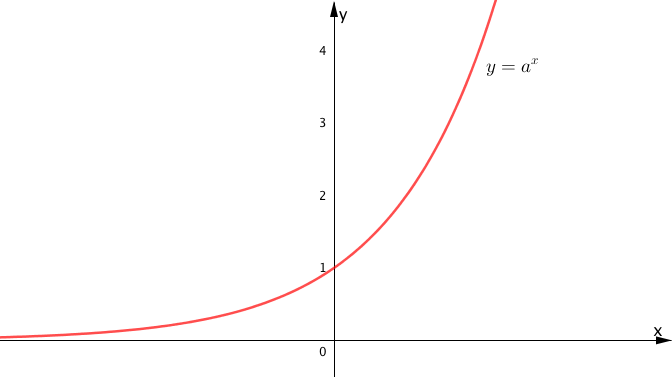
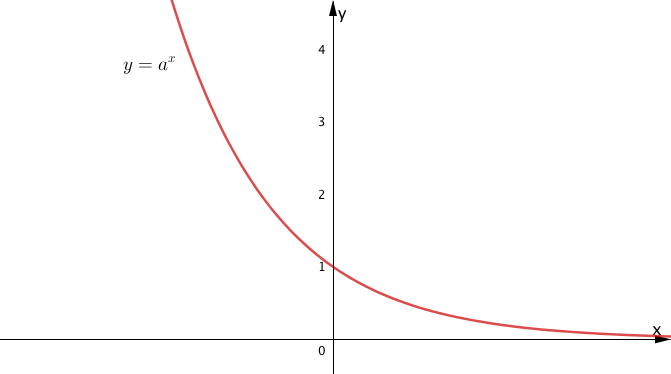
$1 < a $ のときは関数が単調に増加しますが、$0 < a < 1$ のときは関数が単調に減少するという点がグラフの概形の違いとなります。
グラフの概形を代数的に理解する
指数関数のグラフは上で示したような概形となるのですが、なぜこのような形となるか直感的に理解できる方は指数法則をよく理解できていることでしょう。
$1 < a $ の場合の指数関数 $y=2^x$ とを例とし、グラフの概形について代数的に理解しましょう。
$x$ の値を順次変えていき、そのときの $y$ の値を計算すると次のようになります。
$x = 1$ のとき、 $y = 2^1 = 2$
$x = 2$ のとき、 $y = 2^2 = 4$
$x = 3$ のとき、 $y = 2^3 = 8$
$\cdots$
マスマスターの思考回路
$x$ が1増えると $y$ は2倍の値になっています。
これにより、$x$ が増えれば増えるほど $y$ も増え、しかもその増える量自体もどんどん増えていくということが言えます。
よって、関数は常に下に凸な形となります。
これについては直感的にも容易に理解できるかと思いますが、次の内容から指数法則の理解が必要となります。
$x = 0$ のとき、 $y = 2^0 = 1$
マスマスターの思考回路
指数法則より、 $2^0$ は1となります。
0乗が1になることは底が2の場合に限られたことではなく、一般の底 $a$ について成り立ちますので $y=a^x$ の $y$ 切片は1となるというわけです。
$x = -1$ のとき、 $y = 2^{-1} = \left(\cfrac{1}{2}\right)^1 = \cfrac{1}{2}$
マスマスターの思考回路
指数法則によりマイナス乗は逆数を意味することに注意してください。
$x = -2$ のとき、 $y = 2^{-2} = \left(\cfrac{1}{2}\right)^2 = \cfrac{1}{4}$
$x = -3$ のとき、 $y = 2^{-3} = \left(\cfrac{1}{2}\right)^3 = \cfrac{1}{8}$
$\cdots$
マスマスターの思考回路
$x$ が1減ると $y$ は $\frac{1}{2}$ 倍の値になっています。
これにより、$x$ が減れば減るほど $y$ も減っていくことがわかります。
$y$ は $\frac{1}{2}$ 倍（正の数倍）され続けて減っていくので、負の数になることなく限りなく小さくなります。つまり0に無限に近づきます。（無限に近づきますが、ちょうど0となることはありません）
このとき、$y=a^x$ は $y = 0$ （つまり $x$ 軸）を漸近線にもつといいます。
ここまで理解できれば $0 < a < 1$ の場合についても自ずと理解できるかと思いますので、詳しい説明は割愛します。
指数関数とそのグラフの説明の終わりに
いかがでしたか？
今回の要点は次の二点になります。
- 底のとりうる値に関する条件
- グラフの概形
これらは指数関数の次に学ぶ、対数関数とそのグラフを理解するために必須の知識となりますので、しっかり理解しておきましょう。
【基礎】指数関数・対数関数のまとめ
この記事が気に入ったら
「いいね」しよう！
プロフィール
-このサイトの記事を書いている人-
某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。
お問い合わせ
>> お問い合わせ
>> プライバシーポリシー
複素数の関数（複素関数）は高校で学習する範囲を超えていますので、 $y$ の値が実数に限られるような $a > 0$ の範囲のみを対象としようということになります。