【基礎知識】乃木坂46の「いつかできるから今日できる」を数学的命題として解釈する
- 命題
基礎知識
基礎知識
以前、乃木坂46さんの曲「いつかできるから今日できる」を題材にさせていただき、必要十分条件に関する基礎知識について解説しました。
【基礎知識】乃木坂46の「いつかできるから今日できる」から学ぶ必要十分条件
今回はその続編として、命題の逆・裏・対偶について学んでいきましょう。
日本語には「逆もまた真なり」ということわざがありますが、命題でいうところの逆はそれとは意味合いが異なります。
それぞれについて説明していきましょう。
目次
2つの条件$p, ~q$において、命題「$p$ならば$q$」を考えます。
命題「$q$ならば$p$」を命題「$p$ならば$q$」の逆といいます。
つまり、仮定と結論を入れ替えた命題を、もとの命題の逆といいます。
裏を考える前にまず、否定について説明します。
否定とは、それではないもののことです。
つまり「$p$である」の否定は「$p$でない」であり、これを$\overline{p}$と表します。
命題「$\overline{p}$ならば$\overline{q}$」を命題「$p$ならば$q$」の裏といいます。
つまり、仮定と結論を否定した命題を、もとの命題の裏といいます。
命題「$\overline{q}$ならば$\overline{p}$」を命題「$p$ならば$q$」の対偶といいます。
つまり、仮定と結論の逆を否定した命題を、もとの命題の対偶といいます。
必要十分条件についての記事で、命題「$p$ならば$q$」について、$p$と$q$を入れ替えた命題が真であれば$p$は$q$の必要条件であるというお話をしました。
命題「パンダは動物である」は真であり、その逆は「動物はパンダである」になります。
動物には犬や猫など様々な種類がありますので、動物だからといってパンダとは限らないことから、逆は偽になります。
このようにもとの命題と逆の真偽は一致するとは限りません。
逆・裏・対偶について、最も重要なことは、
対偶の真偽はもとの命題の真偽と一致する。
という事です。
証明してみましょう。
命題の真偽は集合を用いて判断することができました。
$p$と$q$の集合を$P, ~Q$とします。
$p$ならば$q$が真であるとき、下のような図で表すことができます。
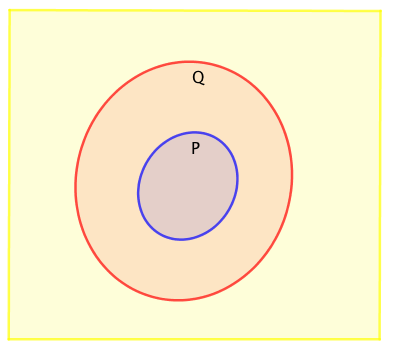
$Q$でない部分(黄色全部)は、$P$でない部分(黄色全部と赤色の一部)に含まれています。
よって、$\overline{q}$ならば$\overline{p}$は真、つまりもとの命題の真偽と対偶の真偽が一致しています。
この場合はさらに3つの場合に分類されます。
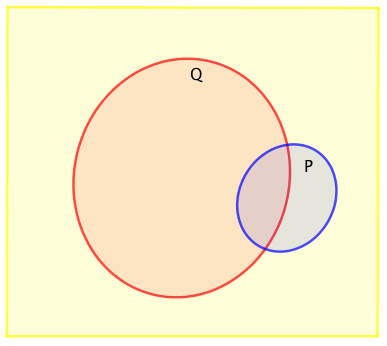
$Q$でない部分(黄色全部と青色の一部)は、$P$でない部分(黄色全部と赤色の一部)に含まれていません。
よって、$\overline{q}$ならば$\overline{p}$は偽、つまりもとの命題の真偽と対偶の真偽が一致しています。

$Q$でない部分(黄色全部と青色全部)は、$P$でない部分(黄色全部と赤色全部)に含まれていません。
よって、$\overline{q}$ならば$\overline{p}$は偽、つまりもとの命題の真偽と対偶の真偽が一致しています。
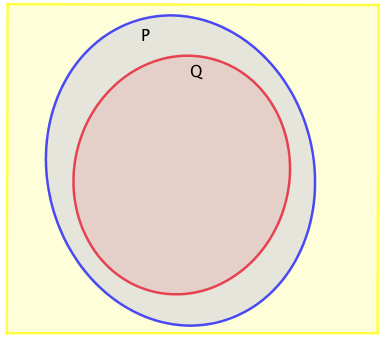
$Q$でない部分(黄色全部と青色の一部)は、$P$でない部分(黄色全部)に含まれていません。
よって、$\overline{q}$ならば$\overline{p}$は偽、つまりもとの命題の真偽と対偶の真偽が一致しています。
以上により「対偶の真偽がもとの命題の真偽と一致すること」が証明されました。
もとの命題を「$p$ならば$q$」とするとき、
逆は「$q$ならば$p$」、
裏は「$\overline{p}$ならば$\overline{q}$」
となります。
ここで逆の対偶を考えてみてください。
逆の対偶は裏と同じであることがわかると思います。
対偶の真偽は一致するので、つまり、逆と裏の真偽は一致することになります。
逆は仮定と結論を入れ替えれば良いだけですが、裏と対偶については否定を考える必要があります。
まずは「いつかできる」と「今日できる」の否定が何であるかを考えましょう。
「いつかできる」の否定を単純に考えると「いつかできない」になります。
しかし、「いつかできない」では意味がわかりませんよね?
単純に考えた否定「いつかできない」を理解しやすいように考えていきましょう。
「いつかできる」とは、今から未来永劫までの期間にはできるということを意味します。
過去には戻れませんから、今から先のことだけを考えます。
時間を数直線にし、「いつかできる」を図にすると下のようになります。

つまり、「いつかできる」ならば、時間軸のどこかに「できた」瞬間の点が存在することになります。
これを否定すると次の図のようになります。

「できた」瞬間の点が存在しなければ「いつかできる」ことにはなりませんので、「いつかできる」の否定は「未来永劫にできない」となります。
これについては簡単で、「今日できない」が成立すれば良いです。
「今日できない」は「いつかできない」とは違って、すんなり状況が把握できます。
このような場合は単純に否定文にするだけで、論理としての否定を作ることができます。
「今日できる」は「いつかできる」とは異なり、「今日」という日しか対象としていませんので、「今日」に限りできなければ良いことになります。
よって「今日できない」と言うだけで「今日できる」ことを否定することができます。
まずは「いつかできるから今日できる」の逆・裏・対偶を文章で表しましょう。次のようになります。
逆:「今日できるからいつかできる」
裏:「未来永劫にできないから今日できない」
対偶:「今日できないから未来永劫にできない」
直感的にすぐに真だとわかるものはどれでしょうか?
この例の場合は、裏:「未来永劫にできないから今日できない」がわかりやすいですね?
そもそもできないものは今日できるはずがありません。よって、裏は真になります。
それと同時に裏の対偶である、逆:「今日できるからいつかできる」も真になります。
マスマスターの思考回路

もとの命題とその対偶については、対偶のほうがわかりやすいかと思います。
一般に、「今日できない」からといって「未来永劫にできない」とは言えないことが多いと思います。
例えば、用事があるとか、体調が優れないとか、いくらでも「今日はできない」理由は思いつきますね?
よって、対偶:「今日できないから未来永劫にできない」は偽であり、元の命題も偽になります。
いかかでしたか?逆・裏・対偶について理解できたでしょうか?
対偶を知ると、「いつかできるから今日できる」は「今日できないから未来永劫にできない」と同じ意味であることが理解できるようになります。
つまり、「いつかできるから今日できる」が偽であることは、「今日できないから未来永劫にできない」を偽だと言っていることと同じになるのです。
これは乃木坂46さんからの「今日できなくても諦めてはいけないよ。ずっとできないわけではないんだから、頑張っていこうよ。」というエールと捉えることができるのです。
「いつかできるから今日できる」が偽であることは残念なことのように聞こえてしまう気がしますが、「今日できないから未来永劫にできない」が偽であることは前向きな気分になりますよね?
両者とも同じことを言っているのに不思議なものですが、「物は言いよう」ということなのでしょう。
これからも乃木坂46さんの「いつかできるから今日できる」を聞いて、日々精進していきましょう。
【基礎】集合と命題のまとめ
この記事が気に入ったら
「いいね」しよう!
-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。
>> お問い合わせ
>> プライバシーポリシー
このように、真偽を考えやすいものから真偽判定し、その対偶も同じ真偽値をとると考えることが問題を解くうえで有効なテクニックになります。