【基礎知識】乃木坂46の「いつかできるから今日できる」を数学的命題として解釈する
- 命題
基礎知識
基礎知識
2次関数の最大・最小
ここでは、高校で学習する関数として基本的なものである二次関数を通じて、最大値・最小値の求め方を説明していきます。
二次関数に限らず、今後学習する様々な関数においても最大値・最小値について問われる事となりますので、しっかり理解しておきましょう。
前提知識として、平方完成と二次関数のグラフに対する理解が必要となりますので、不安な方はまずそちらを復習しておくと良いでしょう。
最大値・最小値とは
関数が値としてとりうる最も大きい値を最大値、最も小さい値を最小値といいます。
マスマスターの思考回路
最大値・最小値がない？
本記事では最大値・最小値の求め方の説明を行うのですが、そもそも最大値・最小値がない場合というのもあります。
どのような場合に最大値・最小値がないということが起こるのでしょうか？
$y=x^2$ と $y=-x^2$ という関数について考えてみましょう。
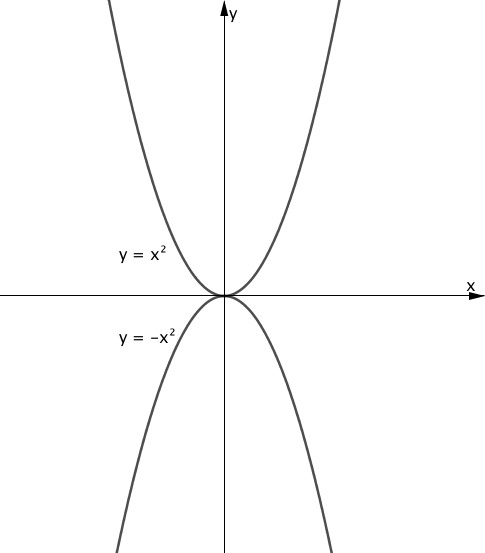
上図のように、 $x$ 座標が原点から離れるほど $y=x^2$ の値は大きくなり、 $y=-x^2$ の値は小さくなります。
どの程度大きい・小さいかというと、それは「無限に」であり、具体的な「値」としてそれらを表現する事ができないものになります。
マスマスターの思考回路
「無限に大きい」や「無限に小さい」は、「値」として表現する事はできないのですが、現段階では深く考える必要はありません。
そういうものだとして流し読みしてしまいましょう。
「値」として表現することができない場合、最大値や最小値は「ない」ものとして扱います。
つまり、$y=x^2$ の最大値および、$y=-x^2$ の最小値は、「ない」となります。
また、 $y=x^2$ のグラフは最も低い位置が原点に一致しますので、最小値は0となります。
同様に、$y=-x^2$ のグラフは最も高い位置が原点に一致しますので、最大値は0となります。
以上により、
$y=x^2$ の最大値はない、最小値は0
$y=-x^2$ の最大値は0、最小値はない
ということになります。
定義域のもとでの最大値・最小値
定義域とは
先の例では最大値・最小値がない場合について説明を行いましたが、最大値・最小値がないということが起こるのは、無限を対象としているからです。
$y=x^2$ という関数について、 $x$ が無限に大きくなれば $y$ も無限に大きくなるという事はその関数を見れば明らかです。（それ自体に何らかの問題があるわけではありません。）
実際の問題では、 $x$ が無限に大きい・小さいという場合を除いてある範囲に限定し、その範囲内での最大値・最小値を考えるという問題が多く扱われることとなります。
この限定されたある $x$ の範囲を定義域といいます。
マスマスターの思考回路
定義域は、中学校で学習した「 $x$ の変域」と同じものになります。
定義域は例として $-2 \leqq x \leqq3$ といった形で表されます。
ある定義域のもとで最大値・最小値を求める
問題 : $y=x^2-4x+2$ について、次の定義域における最大値・最小値を求めよ。
(1) $-1 \leqq x \leqq 1$
(2) $0 \leqq x \leqq 3$
(3) $1 \leqq x \leqq 3$
(4) $1 \leqq x \leqq 4$
(5) $3 \leqq x \leqq 4$
マスマスターの思考回路
関数全般において言えるのですが、最大値・最小値を求める問題では特に、グラフをかくことがとても大切です。
定義域を考える前に $y=x^2-4x+2$ のグラフをかきましょう。
グラフをかくためには平方完成し、頂点の座標を求めておくと良いですね。
【二次関数】平方完成の方法
であり、頂点の座標は $(2, -2)$ であることがわかり、グラフは下のようになります。
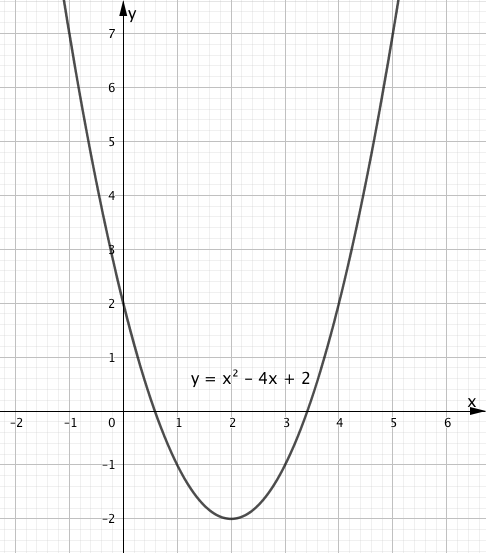
なぜこのようなグラフとなるのかわからない方は、下の記事を参考にしてください。
【基礎】二次関数のグラフ
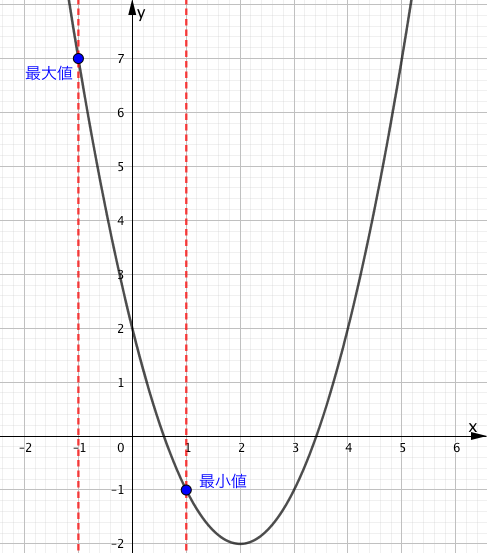
次は、上のグラフに定義域を書き足していきましょう。
(1) $-1 \leqq x \leqq 1$
マスマスターの思考回路
上の図のように、定義域 $-1 \leqq x \leqq 1$ の両端の値を $x$ の定数関数（$x=-1$, $x=1$）としてグラフにかき足す（赤破線）事で、どの範囲が対象となっているかがわかりやすくなります。
赤い破線に挟まれた範囲が定義域が対象としている範囲であり、この範囲内で最も高い（上にある）・低い（下にある）ところがそれぞれ最大値・最小値となります。
実際に問題を解く際にはぜひ上図のような書き方を真似してみてください。
上図により解答は、
$x=-1$ のとき、最大値 $7$
$x=1$ のとき、最小値 $-1$
となります。
マスマスターの思考回路
最大値・最小値の問題は、 $x$ が〜 のとき、最大値（または最小値）〜 のように答えます。
最大・最小をとるときの $x$ の値も記載することが重要です。
以降の問題も(1)と同様に解いていきましょう。
(2) $0 \leqq x \leqq 3$
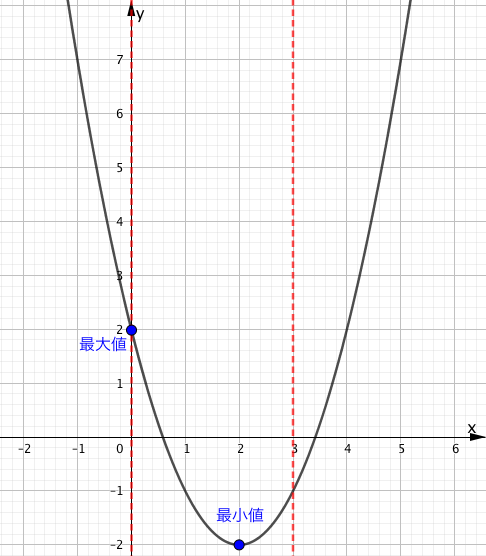
マスマスターの思考回路
この定義域の場合は頂点が定義域内に含まれたことによって、定義域の右端が最小値ではなくなり、頂点が最小値となります。
少しややこしく感じられるところですが、定義域内で一番高い（上にある）、低い（一番低い）ところがそれぞれ最大値・最小値にあたると考えれば視覚的に問題解決することができます。
このために、グラフをかき、目で見てみるという作業がとても重要になるわけです。
上図により解答は、
$x=0$ のとき、最大値 $2$
$x=2$ のとき、最小値 $-2$
となります。
(3) $1 \leqq x \leqq 3$
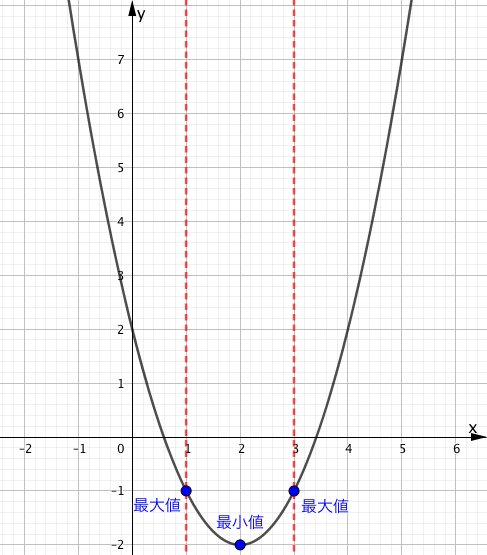
マスマスターの思考回路
この定義域の場合は $x=1$ と $x=3$ のときに共に最も高い位置となっているので、最大値を与える $x$ の値が二つ存在することになります。
この場合、 $x=1, 3$ のとき、最大値〜 といったように解答しましょう。
上図により解答は、
$x=1, 3$ のとき、最大値 $-1$
$x=2$ のとき、最小値 $-2$
となります。
(4) $1 \leqq x \leqq 4$
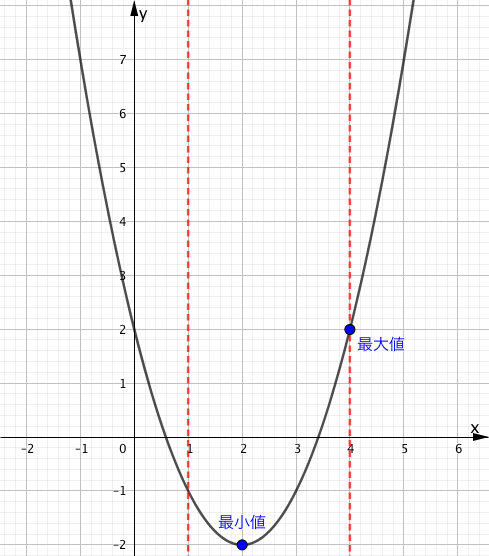
マスマスターの思考回路
今までは定義域の左端で最大値をとっていましたが、軸（頂点の $x$ 座標）が定義域内で相対的に左寄りの配置となったことにより、軸からより遠くに位置する定義域の右端で最大値をとることとなりました。
このように、定義域を少しずつ変化させていくと、最大値をとる位置がすり変わる瞬間が存在します。
この場合でもグラフ化し「一番高い位置はどこか」という観点で考えれば迷うことも少なくなることでしょう。
上図により解答は、
$x=4$ のとき、最大値 $2$
$x=2$ のとき、最小値 $-2$
となります。
(5) $3 \leqq x \leqq 4$
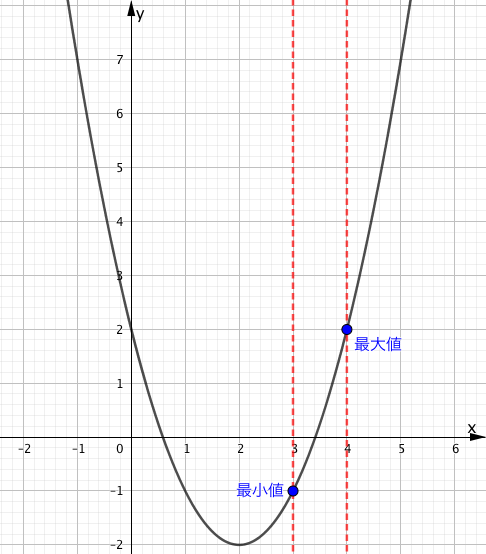
マスマスターの思考回路
頂点が定義域内に含まれなくなったことによって、(1)のようにシンプルな状況に戻りました。
このように、頂点が定義域内に含まれているかどうかは、最大値・最小値を考えるうえで非常に重要な要素となることを覚えておきましょう。
上図により解答は、
$x=4$ のとき、最大値 $2$
$x=3$ のとき、最小値 $-1$
となります。
2次関数の最大・最小の説明のおわりに
いかがでしたか？
少し難しい内容でしたが、グラフをかくことにより視覚的に解決できるようになるということを感じていただけたら良いかと思います。
最大・最小の問題は今後登場する様々な関数でも問われるものですが、基本的な考え方は本記事で説明したとおりのもので解決することが可能です。
今後のためにも、ぜひここでしっかり理解しておくようにしましょう。
【基礎】二次関数のまとめ
この記事が気に入ったら
「いいね」しよう！
プロフィール
-このサイトの記事を書いている人-
某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。
お問い合わせ
>> お問い合わせ
>> プライバシーポリシー
中学校で学習した「変域」に用いられる小さい方の数字が最小値で、大きい方の数字が最大値と考えるとわかりやすいでしょうか。
例えばある関数の変域が $2 \leqq y \leqq 6$ のとき、最小値は$2$ であり、最大値は $6$ であるということになります。
視覚的に考えるともっとわかりやすく、グラフ上の一番高いところが最大値で、一番低いところが最小値となります。