学校や塾では教えてくれない、元塾講師の思考回路の公開

基礎知識

【微分】微分の定義とその意味について

「微分はかすかに分かる、積分は分かったつもり」などと古くから言われますが、そのようにならないよう、定義からしっかり理解しておきましょう。

ここでは微分の定義とその意味について解説していきます。

微分の定義

次の式で表されるf'(x)をf(x)の微分（または導関数）という。

    \begin{eqnarray*} f'(x) = \displaystyle　\lim_{h \to 0} \frac{f(x + h) -f(x)}{h} \end{eqnarray*}

微分の意味

なぜ、微分はそのような式で定義されるのでしょうか？
微分とは何を意味しているのでしょうか？

微分の意味について考えていきましょう。

平均変化率

下図のように、関数y=f(x)上に二点A, Bをとります。

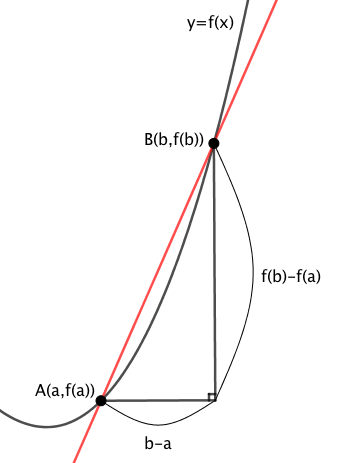
平均変化率

直線ABの傾きは、上図から、

    \begin{eqnarray*}\cfrac{f(b)-f(a)}{b-a} \\\\\end{eqnarray*}

であり、これを、xがaからbまで変化するときのf(x)の平均変化率といいます。

微分係数

次に、上図の点Bを点Aに無限に近づけた場合を考えます。

上の動画から、点Bが点Aに重なるとき、直線ABはy=f(x)の点Aにおける接線になります。
この接線の傾きを、

    \begin{eqnarray*}\lim_{b \to a} \cfrac{f(b)-f(a)}{b-a} \\\\\end{eqnarray*}

と表し、これをx=aにおけるf(x)の微分係数といいます。

ここで、b-a=hとおくと、bがaに近くとき（b \to aと表します）、h \to 0となりますので、微分係数は次の式で表すこともできます。

    \begin{eqnarray*}\lim_{h \to 0} \cfrac{f(a + h)-f(a)}{h} \\\\\end{eqnarray*}

導関数

xの値をaに限定せずにxのままで微分係数の式を表現すると、

    \begin{eqnarray*}\lim_{h \to 0} \cfrac{f(x + h)-f(x)}{h} \\\\\end{eqnarray*}

となり、これをf(x)の微分（または導関数）といい、f'(x)と表します。

これにより、微分の定義は

    \begin{eqnarray*} f'(x) = \displaystyle　\lim_{h \to 0} \frac{f(x + h) -f(x)}{h} \end{eqnarray*}

という式で表されるということになります。

そして微分の意味は、関数のある点における接線の傾きであるといえます。

微分の定義とその意味の説明の終わりに

いかかでしたか？
微分を微かにではなく、しっかり理解できましたか？

微分の考えの根本は、関数上の離れた二点を一点に重なるように無限に近づけることにあります。

これにより、ある点からごく近いある点へどのように移動すればたどり着けるのかが分かるようになり、もともとは離れていた二点の間の部分の関数の挙動を知ることができるようになります。

つまりそれは、微分することにより、関数の概形自体が分かるということを意味します。

微分を用いれば三次関数や四次関数にとどまらず、どのような関数の概形をも知ることができます。

また、一般的に物理法則は微分方程式で記述されますので、それを解くためには微分積分の知識が必須となります。

微分積分は高校数学で最も重要な分野であり、大学入試でも頻出の内容となりますので、十分に理解し使いこなせるようになっておきましょう。

【数II】微分法と積分法のまとめ

基礎知識

微分

プロフィール

-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。

検索

この記事の目次

関連記事

サイドメニュー