【基礎知識】乃木坂46の「いつかできるから今日できる」を数学的命題として解釈する
- 命題
基礎知識
基礎知識
「負の数の平方根はない」という今までの常識を覆し、高校数学では「虚数」というものが登場します。
存在しないと言われていたものが、実は存在しますと今更言われても非常に困惑するかと思います。
数学は数珠つなぎの学問です。ある事実に対して、次のある事実を積み重ねていきます。
この意味では、数学を学ぶ際には数学の歴史を追いかけることになります。
それは、今までは存在しないと思われていたものの存在を認めるという寛容性も持ち合わせていなくてはならないということを意味します。(ちなみに、歴史的には無理数すら存在しないと考えられていた時代がありました。)
非常にとっつきにくい分野になりますが、複素数を用いると多くの自然界の法則を簡潔に記述することができるという点で、複素数はとても重要な道具になります。
複素数が本当に役に立つのは高校を卒業してからになりますので、その基礎を高校時代に固めておきましょう。
目次
$x, y$を実数、$i$を虚数単位$(i=\sqrt{-1})$とし、$z=x+yi$の形で表される数$z$を複素数といいます。
$x$を実部、$y$を虚部といい、実部が0の複素数を順虚数、虚部が0の複素数を実数といいます。
つまり、複素数を学習する以前の全ての数(実数)は、虚部が0の複素数だったというわけです。
複素数$z=x+yi$を従来の$xy$直交座標系の点$(x, y)$を1対1に対応させ、$x$軸を実軸に、$y$軸を虚軸に置き換えた平面を複素数平面といいます。
絶対値とは、「原点からの距離」のことであり、それは複素数平面上の点であっても変わりません。
次の図を考えます。
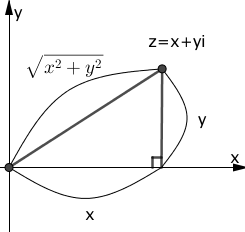
複素数$z=x+yi$の絶対値は三平方の定理から、
と表すことができます。
つまり、複素数の絶対値は負でない実数になります。
複素数$z=x+yi$に対して、$\overline{z}=x-yi$を満たす$\overline{z}$を$z$の共役(きょうやく)複素数といいます。
つまり、ある複素数の虚部の符号を変えたものが共役複素数になります。
$z=x+yi$に対し、$\overline{z}=x-yi$なので、
$y=0$(つまり、$z$が実数)のとき、
$$\begin{array}{rcl} z=x \\\\ \overline{z} = x \end{array}$$なので、
$$\begin{array}{rcl} \overline{z} = z \end{array}$$となります。
また、$x=0$(つまり、$z$が純虚数)のとき、
$$\begin{array}{rcl} z=yi \\\\ \overline{z} = -yi \end{array}$$なので、
$$\begin{array}{rcl} \overline{z} = -z \end{array}$$となります。
以上により、
複素数$z$が実数のとき、
$$\begin{array}{rcl} \overline{z} = z \end{array}$$複素数$z$が純虚数のとき、
$$\begin{array}{rcl} \overline{z} = -z \end{array}$$が成り立ちます。
下図のように、ある複素数とその共役複素数は複素数平面上の実軸に関して対象になります。
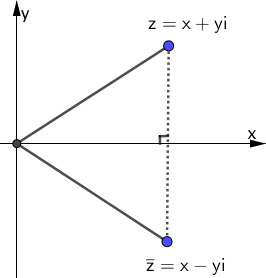
上図により、
が成り立ちます。
共役複素数を用いると、複素数の絶対値と複素数を等式でつなぐことができるようになります。
$z=x+yi$に対し、
$$\begin{array}{rcl} z\overline{z} &=& (x+yi)(x-yi) \\\\ &=& x^2-xyi+xyi-y^2i^2 \\\\ &=& x^2+y^2 \end{array}$$また、
$$\begin{array}{rcl} |z| &=& \sqrt{x^2+y^2} \end{array}$$なので、
が成り立ちます。この式は非常に重要なので覚えておきましょう。
従来の$xy$直交座標系の点$(x, y)$を極座標で表すと下図のようになります。
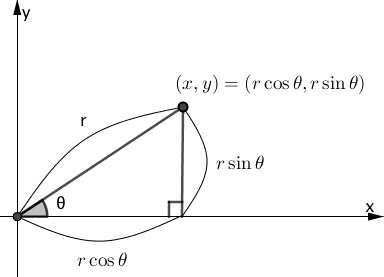
$(x, y) = (r\cos \theta, r\sin \theta)$であり、この点は複素数平面上の点と1対1に対応するので、複素数$z=x+yi$は、
$$\begin{array}{rcl} z &=& x+yi \\\\ &=& r\cos \theta + ir\sin \theta \\\\ &=& r(\cos \theta + i\sin \theta) \end{array}$$よって、
と表すことができ、これを複素数の極形式といいます。
$r(r>0)$は複素数$z$の絶対値であり、$\theta$を偏角といいます。
その他の基礎知識については後日追加予定です。
【基礎知識】複素数平面のまとめ
この記事が気に入ったら
「いいね」しよう!
-このサイトの記事を書いている人-

某国立大工学部卒のwebエンジニアです。
学生時代に塾講師として勤務していた際、生徒さんから「解説を聞けば理解できるけど、なぜその解き方を思いつくのかがわからない」という声を多くいただきました。
授業という限られた時間の中ではこの声に応えることは難しく、ある程度の理解度までに留めつつ、繰り返しの復習で覚えてもらうという方法を採らざるを得ないこともありました。
本ブログでは「数学の問題を解くための思考回路」に重点を置いています。
それらを通じて自らの力で問題を解決する力が身につくお手伝いができれば幸いです。
>> お問い合わせ
>> プライバシーポリシー