勉強の前に

数学の問題をいとも簡単にスラスラ解いている人に対して、頭の中はどうなっているんだろう？と思ったことが誰しも一度はあるかと思います。

しかし、その頭の中では想像を超えるような何かは起きていません。
平たく言うと、解答に至るまでの障害物を順に処理しているだけです。

一方、数学の問題でつまずいてしまう方は、「次に何をしていいかわからない」という状況に陥りがちであると感じます。

しかし、次に何をするかが手順化されていれば、悩むことも少なくなるのではないのでしょうか？

そんな悩みをお持ちの方のためにご朗報、数学の問題の解き方を手順化しました。

数学の問題を解くための手順

上の手順には、公式を知っているなどの最低限の知識が備わっていることが前提になりますが、概ねこの手順を繰り返せば様々な問題が解けるようになると思います。

各手順について説明します。

手順1. 現状を把握すること

問題が難しいほど、三つの手順をくり返す回数が多くなることが一般的だと思います。
その都度状況把握の対象は変わっていきますが、第1回目（＝初見）の現状把握の対象はどんな問題でも共通しています。

それは、問題文を読むことです。

問題文を読むという行為は数学に限ったことではなく、全ての教科で共通する最も基本的な作業ですね。

問題文を読むなんて当たり前すぎて今更言われることじゃない、という意見もおありかと思いますが、問題文を読むことは本当に大切な作業です。

勉強が苦手な方ほど多くみられるのですが、本人はちゃんと読んでいるつもりでも、無意識によくわかっていないところをすっ飛ばして読んでいることがありますので、注意深く問題を読むようにしましょう。

少しずつ、一単語ずつ、ちゃんと意味がわかっているかと自分に問いかけながら読むと良いと思います。

問題文を読んだ時点で意味が理解できていない場合は、それは知識の抜けがあることが原因です。
その時点で問題を解くことをやめ、解説を読むか教科書を読むかなどして、まず知識の補強を行いましょう。

手順2. 答えを求めるために必要なものが何かを考えること

例えば、「三角形の面積を求めよ」という問題が出題されたとします。

この場合、答えを求めるために必要なものは「底辺」と「高さ」になります。

これがわかった時点で、「三角形の面積を求めよ」は「三角形の底辺と高さを求めよ」と考えて差し支えありません。（底辺と高さがわかれば面積はわかるからです。）

すると、当初は「面積」だけを求めればよかったのですが、今は「底辺」と「高さ」の二つを求めなければならないという状況に変わったことになります。

求めるべきものが2つに増えてしまいましたが、その代わり、求めるべきものの内容自体は簡単になっています。

これはつまり、一つの問題が、それよりも簡単ないくつかの問題に分割されたと言うことを意味しています。

そして、分割された問題をさらに分割して、、、ということを続けると、それ以上分割できないほど簡単な、多数の問題に分割されるということになります。

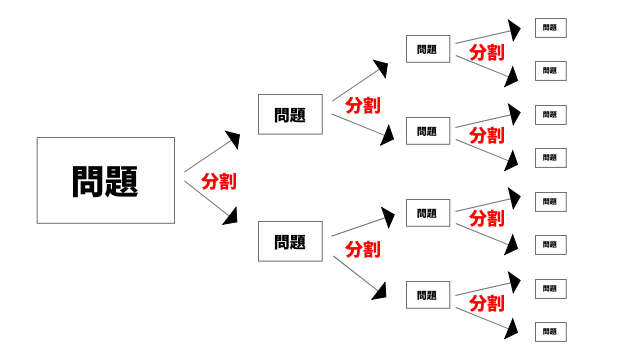
問題が多数あったとしても、このときのその一つ一つはものすごく簡単なはずなので、誰にでも答えられるものになっているはずです。

一般的に「難しい一つ」があるよりも「簡単な多数」がある方が状況として有利と言えると思います。

もちろんその多数がどれほど多数かにもよりますが、個人の力量を超えたものが一つでもある場合にはその問題は解決することができないからです。解決できる可能性を高めるには、自ら問題を簡単にすることが必要です。

さて、一般に問題というものは分割されるのですが、ある答えを求める方法自体を、別の表現に置き換えた場合などを考えると、問題が分割されないこともあります。

例えば、「10を10000回足した結果は？」という問題は、「10 × 10000は？」と同じですね？
この場合、答えに必要なものはかけ算です。
それに気がつけば、問われている内容を言い換えて、問題を簡単にすることができます。
この場合は単なる言い換えなので、問題が分割されない例の一つとなります。

さて、問題が分割されるにしろされないにしろ重要なことは、答えに必要なものがわかれば問題の難易度が下がるということです。

問題の難易度を下げ続ければ、そのときはきっと誰にでも解ける問題になっていることでしょう。

手順3. 答えを求めるために必要なもののうち、現状で求めることが可能なものを求めること

これは手順2で簡単になった問題の答えを実際に求める作業になります。

手順2の説明では、それ以上分割できないほどにまで分割するという話をしましたが、実際にはそこまで分割する（問題を簡単にする）必要はありません。

例えば、の計算結果が必要になった場合、その結果を知っていれば即座にだと答えられます。
知らない場合については、指数法則を利用できれば、なので、と工夫して求めても良いでしょう。はたまた単純に2を10回続けてかけ算して求めるなど、様々な求め方が考えられます。

つまり、どこまで問題を簡単にすれば済むかは、問題を解いている本人の知識や力量に応じて変わるということです。
なんだか元も子もないようなことを言っているように聞こえてしまうような気がしますが、気にやむことではありません。最終的には同じ答えにたどり着きますし、知識や力量は問題を解きながら自然と上がっていきます。

さて、手順3は実際に何らかを求める段階ですので、その何らかを求めるだけです。

その何らかを求められなかった場合は？

手順2の終了時点で自分が答えを求められるレベルにまで問題は簡単になっています。よって、手順3にたどり着いた時点でそれは必ず求められるのです。

求められない場合は、手順2で十分に問題の難易度を下げられていないということになりますので、手順2に戻りましょう。

3つの手順を繰り返そう

手順1〜3を一通り行なっただけでは問題は解決しないこともあります。
そんなときは、手順1〜3を2周3周…と繰り返していきましょう。

3つの手順を繰り返す際に、手順2と3については上で説明しことと同様のことを行えば良いのですが、手順1に関しては少し説明が必要かと思います。

手順1でやるべきことは現状把握であり、問題文を読むことだと言いました。
しかし、2周目以降の手順1では問題文が主な現状把握対象ではありません。

2周目以降の手順1での現状把握対象は、手順3で求めた何らかになります。

手順3で求めた何らかは、最初に問題文を読んだ段階ではわかっていなかったものですよね？
その新しくわかった何らかが今存在していることによって、状況がどう進展したかを把握するのです。

つまり、手順3で何らかが求まったことによって、別の何らかがわかる状況となっているということを把握するのです。

言葉だけではわかりにくいかと思うので、例を挙げましょう。

例えば、という方程式が手元にあったとします。
仮に手順3で、であることがわかったとします。
すると、の値がわかる状況となっていますよね？
最初はわからなかったの値が今ではわかる状況となっているので、状況が進展していますよね？
そのことに気づくことが2周目以降の手順1の役割です。
そして、この例の場合は気づいてしまえば答えは簡単に求まりますね？ついでに求めておきましょう。となります。

イメージがつかめましたか？

手順が進むにつれ、わかるものは増えていきます。

今わかるものは何か？わからないものは何か？何がわかればわからないものがわかるのか？

この問いかけの繰り返しで数学の問題を解くことができます。

そして実は、手順1〜3は、この問いかけを促すためのものなのです。

手順にしたがって実際に問題を解いてみましょう

さて、長々と各手順について説明してきましたが、手順の内容はただ当たり前のことを言っているだけのように思えるかと思います。しかし、当たり前でいいのです。

むしろ根拠のない突飛な考え方をしても、答えが求まるとは思えませんよね？
当たり前の積み重ねこそ、答えを求める唯一の道なのです。

それでは、この手順にしたがって実際に問題を解いてみたいと思います。

手順化された作業を見ていくうえでは、それほど難しくない問題の方が理解しやすいと思いますので、中学範囲の数学を題材としましょう。

この問題について考えていきましょう。

手順1.現状を把握すること

1周目の手順1は、問題を読むことでしたね。
問題を読むと次のことがわかります。

当然ながら、△△であることは、この問題の結論ですので、これを利用して何かを論じることはできません。今は無視しておきましょう。

ということで、現状わかっていることは上で挙げた二点だけとなります。

わかったことが二つあるということは良いのですが、現状では何も状況が進展していません。

などをして、わかったことを実際に使ってみましょう。

今回は図形問題ですので、図に書き込みを追加していきます。

四角形ABCDは平行四辺形であることをどう使うか

平行四辺形が持つ性質は下のように多岐に渡ります。

この全てを図に書き込んでいくと、結論を得るためには不要な情報を書き込んでしまう可能性が高いことと、情報が多くなりすぎて図がわかりにくくなってしまうことが予想されます。

ということで、もう少し後の段階になって、本当に必要な情報が何であるかが明確になってから平行四辺形であることを使うようにしましょう。
現段階では保留としておきます。

AB=APであることをどう使うか

これはとても簡単です。
なぜなら平行四辺形とは異なり、であることに対して「性質」はなく、をそのまま図に反映させるだけで良いからです。

何も気にせず、ABとAPが等しいことを意味する印を図に書き込んでしまいましょう。

すると次の図のようになります。

これにより、△ABPは二等辺三角形であることがわかります。
二等辺三角形の性質より、となりますが、これを図に反映させることは今の段階ではやめておき、保留扱いとしましょう。
なぜなら、どちらの角も証明対象となっている三角形に含まれているものではないので、△△を証明するために直接的には必要な角ではないからです。

ここで、一旦保留していた「四角形ABCDは平行四辺形であること」を思い出しましょう。
辺ABに印がついていますね。ということは平行四辺形の対辺が等しいという性質を使って、辺CDにも同じ印をつけられる状況となっています。

に対して印をつけませんでしたが、辺CDには印をつけて構いません。

なぜなら、辺CDは証明対象となっている三角形に含まれているものになりますので、△△を証明するために直接的に必要になるかもしれない辺であるからです。

これに印をつけると図は下のようになります。

ここまでで、1周目の現状把握により状況を進展させることができました。

次の手順に移りましょう。

手順2.答えを求めるために必要なものが何かを考えること

この問題は証明問題ですので、答え自体は問題文に書いてあります。
「△△」ですね。
合同であることを示すために必要なものは何でしょうか？
それは、合同条件です。

現時点での「答えを求めるために必要なもの」は「合同条件」となります。
しかし、合同条件というものは複数存在しますし、具体的に今何を求めればよいか自体もわかりません。
よって、まだ実際に何かを求めるという手順3に移ることはできません。もっと問題を簡単にしましょう。

合同条件には次の三種類があります。

このうちのいずれかが成立することが言えれば問題は解決します。

ではこの3つのうちのどれが成立するのでしょうか？
現時点ではそれはわかりません。

しかし、証明対象の三角形について、が成立していることはわかっています。
これを次の段階へ進む切り口として進めていきましょう。

現状では、の1組の辺が等しいことがわかっています。
この両端の角についても等しいこということが言えれば「1組の辺とその両端の角がそれぞれ等しい」が成立し、問題が解決します。

辺APと辺DCに対する両端の角が等しいと言える根拠があるのでしょうか？

角APDと角DCAが等しいという根拠があるか？

図を再掲します。

が成立する根拠を提示することはできなさそうです。

といっても、実際にはできるのかもしれません。
しかし、根拠が見つけられていないということは、根拠が存在するかどうかもわからないということです。存在しないかもしれないことには固執せず、他のことを考えると良いでしょう。

ということで、「1組の辺とその両端の角がそれぞれ等しい」が成立する根拠は存在しないことにします。

3つある合同条件のうちどれか一つが成立すれば良いので、他の合同条件が成立するかを調べていきましょう。

他の合同条件について考える

残された合同条件は

• 3組の辺がそれぞれ等しい
• 2組の辺とその間の角がそれぞれ等しい

となりますが、これらが成立するには、最低でも2組の辺が等しいことがわかっていなければなりません。

「最低でも2組の辺が等しいことがわかっていること」には「2組の辺が等しいことがわかっていること」が必要です。
すると、現状ではわかっているので、あと1組の等しい辺を見つければよいことになります。

つまり、「答えを求めるために必要なもの」は「あと1組の等しい辺」となります。

どの合同条件を使うべきかも不明だった状況が、あと1組の等しい辺を見つければよいという状況に変わりました。

実際に求めるのは手順3の段階となります。次の手順に移りましょう。

手順3.答えを求めるために必要なもののうち、現状で求めることが可能なものを求めること

前にもお話ししましたが手順2が十分に行われていれば、手順3ではそれを求めるだけです。

△APDと△DCAにおける「あと1組の等しい辺」はどこでしょうか。
簡単に見つかると思います。共通な辺ADですね。ここに印をつけると図は次のようになります。

手順3で何か1つ求めたら手順1に戻りましょう。2周目の手順1.現状把握を行っていきます。

手順1.現状を把握すること

現状把握なので、現状の図を確認しましょう。

• 3組の辺がそれぞれ等しい
• 2組の辺とその間の角がそれぞれ等しい

のいずれかが成立するには、あと1組の印が適切な箇所につけられれば良いという現状であることがわかるかと思います。

つまり将棋で言うところの王手の段階ですね。

この段階まで進めば、持ち駒を総動員することも一つの戦略です。

ということで、1周目の手順1にて保留していた事柄を使いましょう。

保留していた事柄とは下の二つになります。

の方が簡単なので、こちらを先に使いましょう。
図は次のようになります。

と は証明対象の三角形に含まれている角ではありませんので、これが直接的に合同であることを結論づける要素にはなりません。間接的に役立てることを考えましょう。

次に「四角形ABCDは平行四辺形であること」を使います。

平行線の錯角は等しいので、

この時点で△APDに対して、「2辺とその間の角」の位置関係にあたる辺と角に印がつきました。あとはにと同じ印がつけば合同条件が成立します。

平行四辺形の対角は等しいので、

これで、△と△において、2辺とその間の角が等しいので、△△であることがわかりました。

あとはこれを簡潔にまとめていけば実際の回答ができあがるはずですが、今回は数学を解くための手順についての解説ですので割愛します。

数学の問題を解くための手順のまとめ

再掲となりますが、手順はこちらです。

今回扱った問題は、2周目の手順1で終了してしまいました。
これは、問題文から読み取ることができないので、自分で求める必要があったものが「が共通であること」ただ一つだけだったことによります。
つまり手順3として行うべきものが一つしかなかったということですね。

その意味では手順1と2がいかに大切かがわかる例題だったとも言えるでしょう。

この手順については当然色々なご意見があると思いますが、問題を解いているときに次に何をしていいかわからなくなる方へ少しでも指針になれば幸いです。